Quan sát các giao điểm của đồ thị hàm số y = tanx và đường thẳng y = 1 (Hình 35).

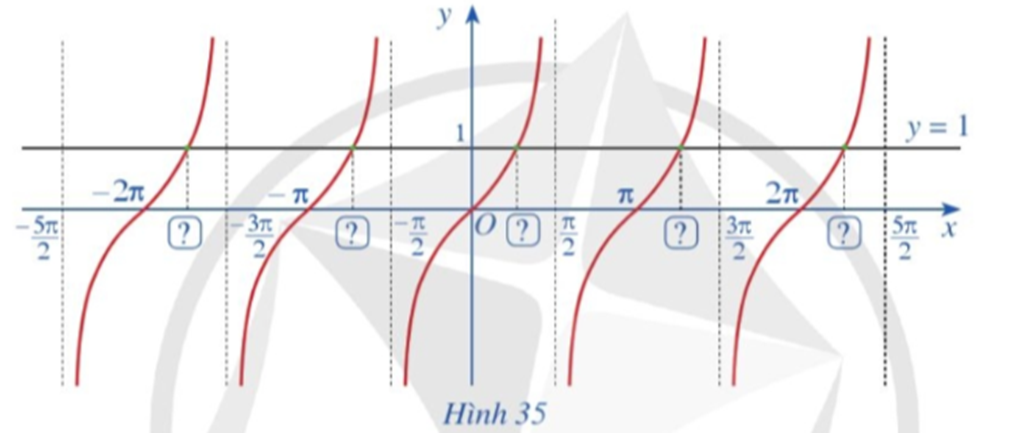
Từ hoành độ giao điểm của đồ thị hàm số y = tanx và đường thẳng y = 1 trên khoảng $\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$, hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó.

Với $x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$ ta thấy tanx = 1 tại $x = \frac{\pi }{4}$.

Do đó đường thẳng y = 1 cắt đồ thị hàm số y = tanx trên khoảng $\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$ tại điểm có hoành độ là $\frac{\pi }{4}$.

Do hàm số y = tanx tuần hoàn với chu kì là π nên đường thẳng y = 1 cắt đồ thị hàm số y = tanx tại các điểm có hoành độ là $x = \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)$.