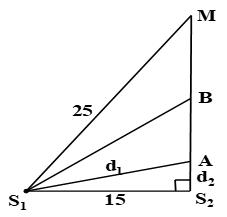
Trong thí nghiệm giao thoa sóng ở mặt chất lỏng, hai nguồn sóng kết hợp đặt tại S₁ và S₂ cách nhau 15 cm, dao động theo phương thẳng đứng với cùng phương trình u = 4cos10πt( mm). Biết tốc độ truyền sóng trên mặt chất lỏng là 15 cm/s. Coi biên độ sóng không đổi. Gọi M là điểm trên mặt chất lỏng sao cho M₁S = 25 cm và MS₂ = 20 cm. Trong khoảng S₂M, hai điểm A và B lần lượt gần S₂ nhất và xa S₂ nhất đều có tốc độ dao động cực đại bằng 80π mm/s. Khoảng cách AB gần nhất với giá trị nào sau đây?

D. 19,1 cm.

$M{S_1}^2 = M{S_2}^2 + {S_1}{S_2}^2 \Rightarrow \Delta M{S_1}{S_2}$ vuông tại ${S_2}$

$\lambda = v.\frac{{2\pi }}{\omega } = 15.\frac{{2\pi }}{{10\pi }} = 3cm$ và $A = \frac{{{v_{\max }}}}{\omega } = \frac{{80\pi }}{{10\pi }} = 8mm = 2a \to$cực đại

Trên $M{S_2}$ thì $\frac{{M{S_1} - M{S_2}}}{\lambda } < k < \frac{{{S_1}{S_2}}}{\lambda } \Rightarrow \frac{{25 - 20}}{3} < k < \frac{{15}}{3}$

$\Rightarrow 1,7 < k < 5 \Rightarrow {k_A} = 4$ và ${k_B} = 2$

${d_1}^2 - {d_2}^2 = {S_1}{S_2}^2 \Rightarrow \left\{ \begin{array}{l}{d_1} - {d_2} = k\lambda \\{d_1} + {d_2} = \frac{{{S_1}{S_2}^2}}{{k\lambda }}\end{array} \right. \Rightarrow {d_2} = \frac{{{S_1}{S_2}^2}}{{2k\lambda }} - \frac{{k\lambda }}{2} = \frac{{{{15}^2}}}{{2k.3}} - \frac{{k.3}}{2} \Rightarrow \left\{ \begin{array}{l}k = 2 \Rightarrow {d_2} = 15,75cm\\k = 4 \Rightarrow {d_2} = 3,375cm\end{array} \right.$

Vậy $AB = 15,75 - 3,375 \approx 12,4cm$. Chọn B