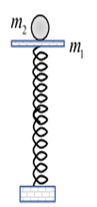
Một con lắc lò xo đặt thẳng đứng gồm lò xo nhẹ có độ cứng $k = 100\,N/m$ và vật nhỏ ${m_1}$ khối lượng $200\,g$. Một đầu lò xo gắn chặt vào sàn. Ban đầu, giữ ${m_1}$ ở vị trí lò xo nén $12\,cm$ (trong giới hạn đàn hồi của lò xo) rồi đặt thêm vật nhỏ ${m_2}$ có khối lượng cũng bằng $200\,g$ lên trên ${m_1}$ như hình bên. Thả nhẹ để các vật bắt đầu chuyển động theo phương thẳng đứng. Vào thời điểm ${t_1}$, vật ${m_2}$ rời khỏi ${m_1}$ chuyển động thẳng đứng lên trên, sau khi rời m₁, m₂ chuyển động ném lên đạt độ cao cực đại vào thời điểm ${t_2}$. Khoảng cách giữa 2 vật tại thời điểm ${t_2}$ có giá trị gần nhất với giá trị nào sau đây?

GĐ1: Hai vật cùng dao động từ M lên đến vị trí tự nhiên

Tại vtcb O nén $\Delta {l_0} = \frac{{\left( {{m_1} + {m_2}} \right)g}}{k} = \frac{{\left( {0,2 + 0,2} \right).10}}{{100}} = 0,04m = 4cm$

$A = 12 - 4 = 8cm$

$\omega = \sqrt {\frac{k}{{{m_1} + {m_2}}}} = \sqrt {\frac{{100}}{{0,2 + 0,2}}} = 5\sqrt {10}$ (rad/s)

$v = \omega \sqrt {{A^2} - \Delta l_0^2} = 5\sqrt {10} .\sqrt {{8^2} - {4^2}} = 20\sqrt {30}$ (cm/s)

GĐ2: Tại vttn thì lực đàn hồi hướng xuống nên vật m₂ tách khỏi m₁

*Vật m₂ bị ném lên thẳng đứng đến khi dừng lại lần đầu thì $t = \frac{v}{g} = 0,02\sqrt {30} s$

*Vật m₁ dao động điều hòa quanh vị trí cân bằng mới O₁ nén

$\Delta {l_1} = \frac{{{m_1}g}}{k} = \frac{{0,2.10}}{{100}} = 0,02m = 2cm$ và \({\omega _1} = \sqrt {\frac{k}{{{m_1}}}} = \sqrt {\frac{{100}}{{0,2}}}  = 10\sqrt 5 \) (rad/s)

${A_1} = \sqrt {\Delta l_1^2 + {{\left( {\frac{v}{{{\omega _1}}}} \right)}^2}} = \sqrt {{2^2} + {{\left( {\frac{{20\sqrt {30} }}{{10\sqrt 5 }}} \right)}^2}} = 2\sqrt 7 cm$

Chọn gốc tọa độ tại vị trí cân bằng mới O₁, chiều dương hướng lên

$\left\{ \begin{array}{l}{x_1} = {A_1}\cos \left( {{\omega _1}t - \arccos \frac{{\Delta {l_1}}}{{{A_1}}}} \right) = 2\sqrt 7 \cos \left( {10\sqrt 5 .0,02\sqrt {30} - \arccos \frac{2}{{2\sqrt 7 }}} \right) \approx 1,5865cm\\{x_2} = \Delta {l_1} + vt - \frac{1}{2}g{t^2} = 2 + 20\sqrt {30} .0,02\sqrt {30} - \frac{1}{2}.1000.{\left( {0,02\sqrt {30} } \right)^2} = 8cm\end{array} \right.$

${x_2} - {x_1} = 8 - 1,5865 = 6,4135cm$. Chọn B