Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình là

Trả lời

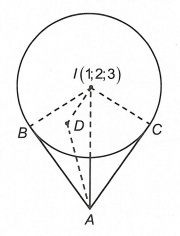
Gọi I là tâm mặt cầu thì $I\left(1;2;3\right)$ .

Gọi O là giao điểm của mặt phẳng $\left(BCD\right)$  và đoạn AI.

Vì theo giả thiết $AB=AC=AD$  và $IB=IC=ID=\sqrt{\frac{14}{3}}$  nên AI vuông góc với mặt phẳng $\left(BCD\right)$  tại O. Khi đó O là tâm đường tròn ngoại tiếp $\Delta BCD$ .

Đặt $AI=x\left(x>\sqrt{\frac{14}{3}}\right)$ .

Ta có $AB=\sqrt{A{I}^2-I{B}^2}=\sqrt{x^2-\frac{14}{3}}$

$$\begin{gathered} I{B}^2=IO.IA\Rightarrow OI=\frac{14}{3x}\Rightarrow OB=\sqrt{I{B}^2-I{O}^2}=\sqrt{\frac{14}{3}-{\left(\frac{14}{3x}\right)}^2} \\ \Rightarrow B{D}^2=O{B}^2+O{D}^2-2OB.OD.\cos 120°=3O{B}^2 \\ \Rightarrow BD=\sqrt{3}OB\Rightarrow BD=\sqrt{3}OB=\sqrt{3.\left(\frac{14}{3}-\frac{196}{9x^2}\right)} \end{gathered}$$

Do ABCD là tứ diện đều nên

$$\begin{gathered} AB=BD\Rightarrow \sqrt{x^2-\frac{14}{3}}=\sqrt{3\left(\frac{14}{3}-\frac{196}{9x^2}\right)}\iff x^2-\frac{14}{3}=14-\frac{196}{3x^2} \\ 3x^4-56x^2+196=0\iff \left[\begin{array}{l}{x}^2=\frac{14}{3}\\ x^2=14\end{array}\right.\Rightarrow x=\sqrt{14} \end{gathered}$$

$A\in d$ nên $A\left(4+3t;4+2t;4+t\right)$ .

Suy ra $AI=\sqrt{14}\iff \sqrt{{\left(4+3t-1\right)}^2+{\left(4+2t-2\right)}^2+{\left(4+t-3\right)}^2}=\sqrt{14}$

$\iff \left|t+1\right|=1\iff \left[\begin{array}{l}t=0\\ t=-2\end{array}\right.\Rightarrow \left[\begin{array}{l}A\left(4;4;4\right)\\ A\left(-2;0;2\right)\end{array}\right.$

Do $x_0>0$  nên điểm A có tọa độ $A\left(4;4;4\right)$ .

Suy ra $P=12$ .

Chọn C.