Trong không gian Oxyz, cho mặt cầu (S) có phương trình x^2+y^2+z^2-4x+2y-2z-3=0
200
24/04/2024
Trong không gian Oxyz, cho mặt cầu (S) có phương trình và điểm . Một đường thẳng d thay đổi luôn đi qua A và luôn cắt mặt cầu tại hai điểm phân biệt .
Tính giá trị nhỏ nhất của biểu thức .
B. .
C. .
D. .
Trả lời
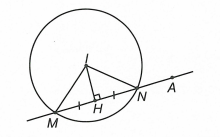
Mặt cầu có tâm , bán kính .
Ta có: nên A nằm ngoài mặt cầu .
Ta lại có: .
Đặt .
Mà .
Do đó: với .
Ta có: với .
Do đó: .
Dấu “=” xảy ra thẳng hàng và .
Chọn C.

