Trong không gian Oxyz, cho hai điểm A(9,6,11), B(5,7,2) và điểm M di động
146
24/04/2024
Trong không gian Oxyz, cho hai điểm A(9,6,11), B(5,7,2) và điểm M di động trên mặt cầu (S):(x−1)2+(y−2)2+(z−3)2=36 .
Giá trị nhỏ nhất của AM+2MB bằng
B. 2√26 .
C. 2√29 .
D. √102 .
Trả lời
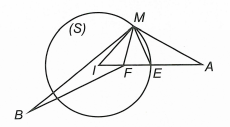
Mặt cầu (S):(x−1)2+(y−2)2+(z−3)2=36 có tâm I(1;2;3) và bán kính R=6 .
Ta có IA=12=2R .
Gọi E là giao điểm của IA và mặt cầu (S) suy ra E là trung điểm của IA nên E(5;4;7) .
Gọi F là trung điểm của IE suy ra F(3;3;5) .
Xét ΔMIF và ΔAIM có ^AIM chung và IFIM=IMIA=12 .
Suy ra ΔMIFΔAIM(c.g.c)⇒MAMF=AIMI=2⇒MA=2MF .
Do đó AM+2MB=2(MF+MB)≥2BF=2√29 (theo bất đẳng thức tam giác).
Dấu “=” xảy ra khi M là giao điểm FB và mặt cầu (S) .
Chọn C.

