Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):(x-1)^2+(y+1)^2+(z-2)^2=9  và

Trả lời

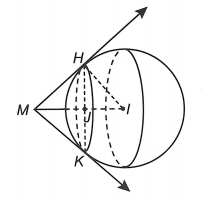
Ta có mặt cầu $\left(S\right)$  có tâm $I\left(1;-1;2\right)$  và bán kính $R=3$ .

Khi đó $IM=5>R\Rightarrow M$  nằm ngoài mặt cầu.

Phương trình đường thẳng MI là $\left\{\begin{array}{l}x=1\\ x=-1+4t\\ z=2-3t\end{array}\right.$ .

Tâm $J\left(a;b;c\right)$  nằm trên MI nên $J\left(1;-1+4t;2-3t\right)$ .

Xét $\Delta MHI$  vuông tại H có

$MI=5;IH=3\Rightarrow MH=\sqrt{M{I}^2-H{I}^2}=4$

Mặt khác $\left\{\begin{array}{l}M\left(1;3;-1\right)\\ J\left(1;-1+4t;2-3t\right)\end{array}\right.\Rightarrow MJ=\sqrt{{\left(-4+4t\right)}^2+{\left(3-3t\right)}^2}$ .

$$\begin{gathered} MJ.MI=M{H}^2\Rightarrow MJ=\frac{16}{5} \\ \iff {\left(-4+4t\right)}^2+{\left(3-2t\right)}^2=\frac{256}{25} \\ \iff 25t^2-50t+\frac{369}{25}=0\iff \left[\begin{array}{l}t=\frac{9}{25}\\ t=\frac{41}{25}\end{array}\right. \end{gathered}$$

Suy ra $J\left(1;\frac{11}{25};\frac{23}{25}\right)$  hoặc $J\left(1;\frac{139}{25};\frac{-73}{25}\right)$ .

+) Với $J\left(1;\frac{11}{25};\frac{23}{25}\right)$  thì $IJ=\frac{9}{5}<IM$  (nhận).

+) Với $J\left(1;\frac{139}{25};\frac{-73}{25}\right)$  thì $IJ=\frac{41}{5}>IM$  (loại).

Vậy $J\left(1;\frac{11}{25};\frac{23}{25}\right)$  nên $2a+b+c=\frac{84}{25}$ .

Chọn C.