Trong không gian với hệ tọa độ Oxyz, cho ba điểm P,Q,R lần lượt di động trên ba trục tọa độ $Ox,Oy,Oz$  (không trùng với gốc tọa độ O) sao cho $\frac{1}{O{P}^2}+\frac{1}{O{Q}^2}+\frac{1}{O{R}^2}=\frac{1}{8}$ . Biết mặt phẳng $\left(PQR\right)$  luôn tiếp xúc với mặt cầu $\left(S\right)$  cố định. Đường thẳng $\left(d\right)$  thay đổi nhưng luôn đi qua $M\left(\frac{1}{2};\frac{\sqrt{3}}{2};0\right)$  và cắt $\left(S\right)$  tại hai điểm $A,B$  phân biệt. Diện tích lớn nhất của $\Delta AOB$  là

A. $\sqrt{15}$ .

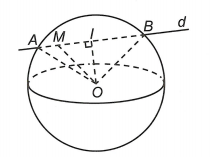
Gọi H là hình chiếu vuông góc của điểm O trên mặt phẳng $\left(PQR\right)$ .

Dễ thấy $\frac{1}{O{H}^2}=\frac{1}{O{P}^2}+\frac{1}{O{Q}^2}+\frac{1}{O{R}^2}\Rightarrow \frac{1}{O{H}^2}=\frac{1}{8}\Rightarrow OH=2\sqrt{2}$ .

Khi đó $\left(PQR\right)$  luôn tiếp xúc với mặt cầu (S) tâm O, bán kính $R=2\sqrt{2}$ .

Ta có $OM=\sqrt{\frac{1}{4}+\frac{3}{4}+0}=1<R$  nên điểm M nằm trong mặt cầu $\left(S\right)$ .

Gọi I là trung điểm của AB, do $\Delta OAB$  cân tại O nên $S_{\Delta OAB}=\frac{1}{2}OI.AB$ .

Đặt $OI=x$ . Vì $OI\le OM$  nên $0<x\le 1$  và $AB=2\sqrt{8-x^2}$ .

Ta có $S_{\Delta OAB}=\frac{1}{2}x.2\sqrt{8-x^2}=x\sqrt{8-x^2}=\sqrt{8x^2-x^4}$ .

Xét hàm số $f\left(x\right)=8x^2-x^4,0<x\le 1$ .

Vì $f^{\text{'}}\left(x\right)=4x\left(4-x^2\right)>0$  với mọi $x\in \left(0;1\right]$  nên $f\left(x\right)\le f\left(1\right)=7$ .

Suy ra diện tích của $\Delta OAB$  lớn nhất bằng $\sqrt{7}$  đạt được khi M là trung điểm của AB.

Chọn D.