Trong không gian Oxyz. Cho điểm E(1,1,1), mặt cầu (S):x^2+y^2+z^2=4  và mặt phẳng

Trả lời

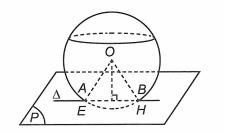
Gọi $\overrightarrow{u}=\left(a;b;c\right)$  là một vectơ chỉ phương của $∆$ với $a^2+b^2+c^2>0$ .

Ta có $\overrightarrow{n_P}=\left(1;-3;5\right)$ .

Vì $\Delta \subset \left(P\right)$  nên $\overrightarrow{u}\perp \overrightarrow{n_P}\Rightarrow \overrightarrow{u}.\overrightarrow{n_P}=0\iff a-3b+5c=0\iff a=3b-5c$ .(1)

Mặt cầu $\left(S\right)$  có tâm $O\left(0;0;0\right)$  và bán kính $R=2$ .

Gọi H là hình chiếu vuông góc của O trên AB

Ta có $\Delta OAB$  là tam giác đều cạnh R nên $OH=\frac{R\sqrt{3}}{2}=\sqrt{3}$ .

Suy ra khoảng cách từ O đến đường thẳng $∆$ bằng $OH=\sqrt{3}$ .

Khi đó $\frac{\left|\left[\overrightarrow{u},\overrightarrow{OE}\right]\right|}{\left|\overrightarrow{u}\right|}=\sqrt{3}$

$\iff {\left(a-b\right)}^2+{\left(b-c\right)}^2+{\left(c-a\right)}^2=3\left(a^2+b^2+c^2\right)$

$\iff {\left(a+b+c\right)}^2=0\iff a+b+c=0$(2)

Thay (1) vào (2) ta được:

$3b-5c+b+c=0\iff b=c\Rightarrow a=-2c$

Thay $c=-1$  thì $b=-1$  và $a=2$ .

Ta được một vectơ chỉ phương của $∆$ là $\overrightarrow{u}=\left(2;-1;-1\right)$

Vậy phương trình của đường thẳng $∆$ là $\left\{\begin{array}{l}x=1+2t\\ y=1-t\\ z=1-t\end{array}\right.$ .

Chọn C.