Trong Hình 8 cho tam giác BEC (BE < BC) chứng minh rằng: EB = EC . ED
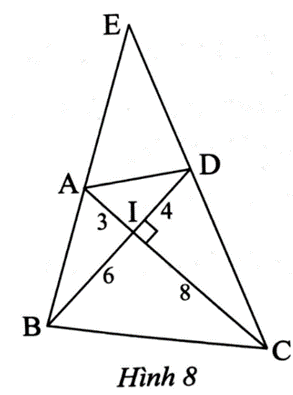
Trong Hình 8, cho tam giác BEC (BE < BC). Cho biết AC ⊥ BD, chứng minh rằng:
EA . EB = EC . ED.
Ta có ∆AIB ᔕ ∆DIC, suy ra \[\widehat {ABI} = \widehat {DCI}\].
Xét ∆EDB và ∆EAC có
\[\widehat E\] chung và \[\widehat {ABI} = \widehat {DCI}\].
Do đó ∆EDB ᔕ ∆EAC (g.g).
Suy ra \[\frac{{ED}}{{EA}} = \frac{{EB}}{{EC}}\]. Do đó EA . EB = EC . ED (đpcm).