AE² = EC . FH.

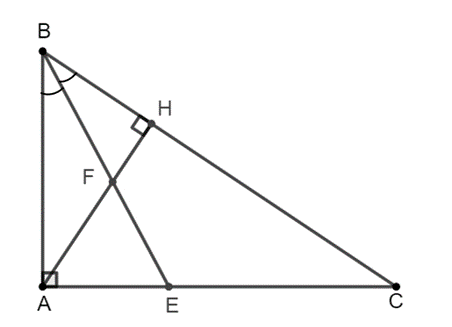
Xét ∆ABC có BE là tia phân giác của \[\widehat B\], suy ra \[\frac{{AB}}{{BC}} = \frac{{AE}}{{EC}}\]  (1)

Xét ∆ABH có BF là tia phân giác của \[\widehat B\], suy ra \[\frac{{FH}}{{AF}} = \frac{{BH}}{{AB}}\] (2)

Xét ∆ABH vuông tại H và ∆ABC vuông tại A có \[\widehat B\] chung.

Do đó ∆ABH ᔕ ∆CBA, suy ra \[\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\]         (3)

Từ (1); (2) và (3) suy ra \[\frac{{AE}}{{EC}} = \frac{{FH}}{{AF}}\].

Do đó AE . AF = EC . FH.

Mà AE = AF, suy ra AE² = EC . FH (đpcm).