Cho tam giác ABC vuông tại A. Tia phân giác của \[\widehat A\] cắt cạnh huyền BC tại M. Qua M kẻ đường thẳng vuông góc với BC và cắt AC tại N. Chứng minh rằng:

MN = MB.

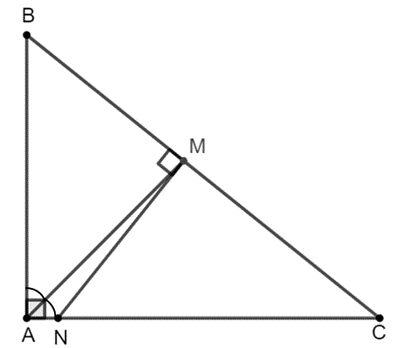
Ta có ∆MNC ᔕ ∆ABC, suy ra \[\frac{{MN}}{{AB}} = \frac{{MC}}{{AC}}\]       (1)

Xét ∆ABC có AM là phân giác của \[\widehat A\] có

\[\frac{{MB}}{{MC}} = \frac{{AB}}{{AC}}\], suy ra \[\frac{{MB}}{{AB}} = \frac{{MC}}{{AC}}\]           (2)

Từ (1) và (2), suy ra \[\frac{{MB}}{{AB}} = \frac{{MN}}{{AB}}\].

Do đó MN = MB (đpcm).