Chứng minh rằng tam giác ABH tam giác MNK. Tính tỉ số AH/MK = 2/3
Cho ∆ABC ᔕ ∆MNP theo tỉ số đồng dạng k=ABMN=23. Kẻ đường cao AH của tam giác ABC và đường cao MK của tam giác MNP.
a) Chứng minh rằng ∆ABH ∆MNK. Tính tỉ số AHMK=23.
Cho ∆ABC ᔕ ∆MNP theo tỉ số đồng dạng k=ABMN=23. Kẻ đường cao AH của tam giác ABC và đường cao MK của tam giác MNP.
a) Chứng minh rằng ∆ABH ∆MNK. Tính tỉ số AHMK=23.
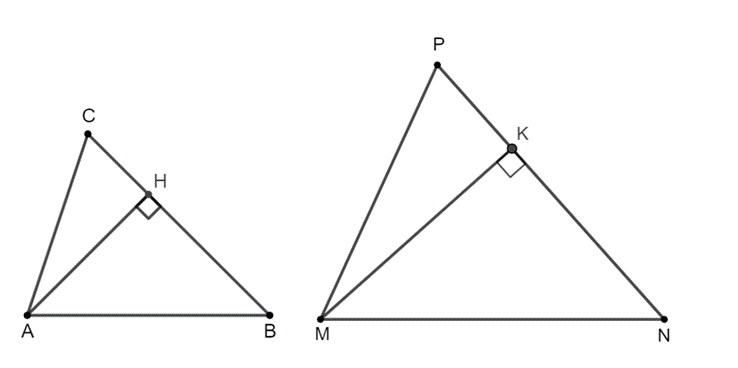
Ta có ∆ABC ᔕ ∆MNP, suy ra ˆB=ˆN
Xét ∆ABH vuông tại H và ∆MNK vuông tại K có ˆB=ˆN.
Do đó ∆ABH ᔕ ∆MNK (g.g).
Suy ra AHMK=ABMN=23.
Vậy AHMK=23.