Câu hỏi:
21/12/2023 78
Hàm số nào sau đây là hàm số bậc hai?
Hàm số nào sau đây là hàm số bậc hai?
A. y = x3 + x2 – 2022;
B. y = 2022x + 2021;
C. y = 2021;
D. y = x2 – 2022.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
Hàm số y = x3 + x2 – 2022 có bậc cao nhất là bậc 3, nên đây không hàm số bậc hai.
Hàm số y = 2022x + 2021 có bậc cao nhất là bậc 1, nên đây không hàm số bậc hai.
Hàm số y = 2021 là hàm hằng.
Hàm số y = x2 – 2022 là hàm số bậc hai vì nó có dạng y = ax2 + bx + c với a = 1, b = 0 và c = – 2022.
Đáp án đúng là: D
Hàm số y = x3 + x2 – 2022 có bậc cao nhất là bậc 3, nên đây không hàm số bậc hai.
Hàm số y = 2022x + 2021 có bậc cao nhất là bậc 1, nên đây không hàm số bậc hai.
Hàm số y = 2021 là hàm hằng.
Hàm số y = x2 – 2022 là hàm số bậc hai vì nó có dạng y = ax2 + bx + c với a = 1, b = 0 và c = – 2022.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Đồ thị hàm số y = 3x2 + 4x + 3 nhận đường thẳng nào dưới đây làm trục đối xứng?
Đồ thị hàm số y = 3x2 + 4x + 3 nhận đường thẳng nào dưới đây làm trục đối xứng?
Câu 2:
Cho hàm số y = f(x) xác định trên khoảng (a; b). Hàm số y = f(x) gọi là nghịch biến trên khoảng (a; b) khi?
Cho hàm số y = f(x) xác định trên khoảng (a; b). Hàm số y = f(x) gọi là nghịch biến trên khoảng (a; b) khi?
Câu 3:
Đồ thị hàm số bậc hai y = ax2 + bx + c (a ≠ 0) là một đường parabol có đỉnh là điểm với toạ độ là:
Đồ thị hàm số bậc hai y = ax2 + bx + c (a ≠ 0) là một đường parabol có đỉnh là điểm với toạ độ là:
Câu 6:
Dựa vào đồ thị hàm số bậc hai y = f(x) trong hình dưới đây. Tập nghiệm nào sau đây là tập nghiệm của bất phương trình f(x) ≤ 0?
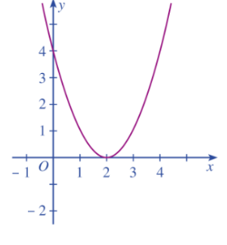
Dựa vào đồ thị hàm số bậc hai y = f(x) trong hình dưới đây. Tập nghiệm nào sau đây là tập nghiệm của bất phương trình f(x) ≤ 0?


