Cho tam giác đều ABC có độ dài cạnh là 6 cm. Trên tia BA, CA lần lượt lấy điểm D, E sao cho AD = AE = 2 cm (Hình 12).
Tính độ dài đoạn thẳng CD (làm tròn kết quả đến hàng phần mười của centimét).
Kẻ DH vuông góc với CE tại H.
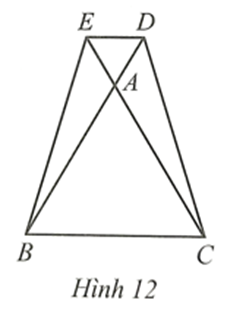
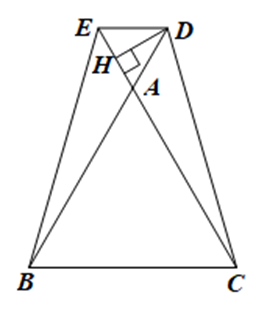
Xét ∆ADH vuông tại H và ∆EDH vuông tại H có:
ED = AD (chứng minh câu a), cạnh DH chung
Do đó ∆ADH = ∆EDH (cạnh huyền – cạnh góc vuông).
Suy ra AH = EH (hai cạnh tương ứng)
Hay H là trung điểm của AE nên \(AH = EH = \frac{{AE}}{2} = \frac{2}{2} = 1{\rm{\;}}\;\;\left( {{\rm{cm}}} \right)\).
Áp dụng định lý Pythagore cho tam giác ADH vuông tại H, ta có: AD2 = AH2 + DH2.
Suy ra DH2 = AD2 ‒ AH2 = 22 ‒ 12 = 3.
Ta có: CH = AC + AH = 6 + 1 = 7 cm.
Áp dụng định lý Pythagore cho tam giác CDH vuông tại H, ta có: CD2 = CH2 + DH2.
Suy ra CD2 = 72 + 3 = 49 + 3 = 52.
Vậy \(CD = \sqrt {52} \approx 7,2\;\;\left( {{\rm{cm}}} \right)\).