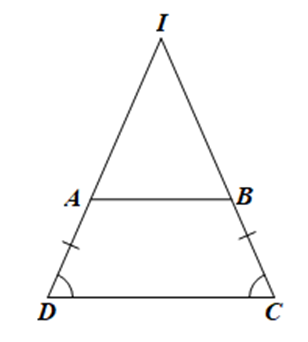
Gọi I là giao điểm của AD và BC.

Do \(\widehat C = \widehat D\) nên tam giác ICD cân tại I. Suy ra ID = IC.

Mà AD = BC; ID = IA + AD; IC = IB + BC

Suy ra IA = IB.

Do đó, tam giác IAB cân tại I.

Xét DICD cân tại I có \(\widehat D = \widehat C = \frac{{180^\circ - \widehat I}}{2}\).

Xét DIAB cân tại I có \(\widehat {IAB} = \widehat {IBA} = \frac{{180^\circ - \widehat I}}{2}\).

Do đó \(\widehat {IAB} = \widehat D\), mà \(\widehat {IAB}\) và \(\widehat D\) nằm ở vị trí đồng vị

Suy ra AB // CD.

Tứ giác ABCD có AB // CD và \(\widehat C = \widehat D\) nên ABCD là hình thang cân.