Cho hình thang cân ABCD có AB // CD, AB < CD, hai đường chéo AC và BD cắt nhau tại P, hai cạnh bên AD và BC kéo dài cắt nhau tại Q. Chứng minh PQ là đường trung trực của hai đáy hình thang cân ABCD.
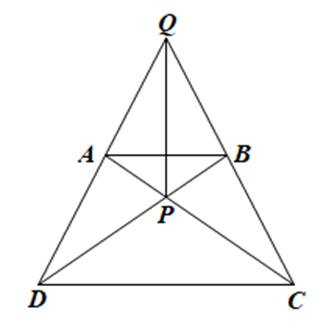
• Xét ∆ACD và ∆BDC có:
AD = BC;
^ADC=^BCD (do ABCD là hình thang cân);
CD là cạnh chung
Do đó ∆ACD = ∆BDC (c.g.c).
Suy ra ^ACD=^BDC (hai góc tương ứng)
Tam giác PCD có ^PCD=^PDC nên là tam giác cân tại P.
Suy ra PC = PD.
Mà AC = BD (do ∆ACD = ∆BDC);
AC = AP + PC; BD = PD + BD
Suy ra PA = PB nên P nằm trên đường trung trực của AB (1)
• Do AB // CD nên ^QAB=^ADC;^QBA=^BCD (các cặp góc đồng vị).
Mặt khác, ^ADC=^BCD (do ∆ACD = ∆BDC) nên ^QAB=^QBA.
Do đó, tam giác QAB cân tại Q.
Suy ra QA = QB nên Q nằm trên đường trung trực của AB (2)
Từ (1) và (2) suy ra PQ là đường trung trực của AB.
• Ta có: AD = BC và PA = PB suy ra QD = QC.
Do đó Q nằm trên đường trung trực của CD.
Mặt khác PC = PD (chứng minh trên) nên P cũng nằm trên đường trung trực của CD.
Suy ra PQ là đường trung trực của CD.
Vậy PQ là đường trung trực của cả hai đoạn AB và CD.