Chứng minh tứ giác BMNC là hình thang cân
Cho tam giác ABC cân tại A. Lấy điểm M, N lần lượt trên cạnh AB, AC sao cho AM = AN.
Chứng minh tứ giác BMNC là hình thang cân.
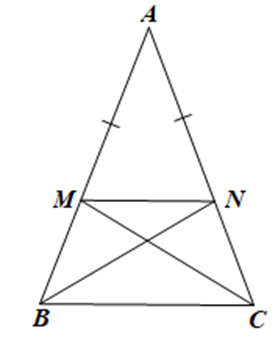
Do AM = AN nên ∆AMN cân tại A.
Xét ∆AMN cân tại A có: ^AMN=^ANM=180∘−ˆA2.
Xét ∆ABC đều hay cũng cân tại A có ^ABC=^ACB=180∘−ˆA2.
Suy ra ^AMN=^ABC(=180∘−ˆA2)
Mà ^AMN và ^ABC nằm ở vị trí đồng vị, suy ra MN // BC.
Tứ giác BMNC có MN // BC và ^MBC=^NCB nên BMNC là hình thang cân.