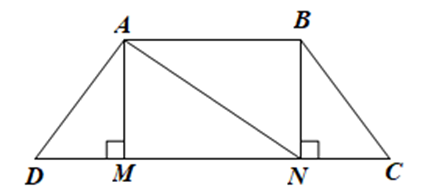
• Xét ∆ADM vuông tại M và ∆BCN vuông tại N có:
AD = BC; \(\widehat {ADM} = \widehat {BCN}\) (do ABCD là hình thang cân)
Do đó ∆ADM = ∆BCN (cạnh huyền – góc nhọn).
Suy ra AM = BN; DM = CN (các cặp cạnh tương ứng)
• Do AB // CD mà BN ⊥ CD nên BN ⊥ AB, do đó tam giác ABN vuông tại B.
Xét ∆ABN vuông tại B và ∆NMA vuông tại M có:
\(\widehat {BAN} = \widehat {MNA}\) (2 góc so le trong của AB // CD);
Cạnh AN chung
Do đó ∆ABN = ∆NMA (cạnh huyền – góc nhọn).
Suy ra AB = NM (hai cạnh tương ứng)
Mà AB = 3 cm nên NM = 3 cm.
• Ta có DM + NM + CN = CD và DM = CN nên 2DM + 3 = 6.
Suy ra DM = 1,5 cm.
Mà DN = DM + NM = 1,5 + 3 = 4,5 cm.
Trong tam giác ADM vuông tại M, ta có: AD2 = AM2 + DM2.
Suy ra AM2 = AD2 ‒ DM2 = 2,52 ‒ 1,52 = 4.
Vậy \(AM = \sqrt 4 = 2\;\;\left( {{\rm{cm}}} \right)\).