Tính chiều cao và diện tích của một tam giác đều có cạnh bằng 4 cm.

Trả lời

Lời giải

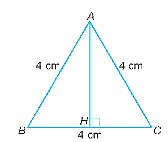
Xét tam giác đều ABC có cạnh AB = AC = BC = 4 cm.

Kẻ đường cao AH của tam giác đều ABC.

Khi đó, đường cao AH đồng thời là đường trung tuyến. Do đó, ta có:

BH = \(\frac{1}{2}\)BC = \(\frac{1}{2}.4\)= 2 (cm).

Áp dụng định lý Pythagore vào tam giác ABH vuông tại H có:

AH² + BH² = AB²

Suy ra AH² = AB² – BH² = 4² – 2² = 12.

Do đó, \(AH = \sqrt {12} \) = \(2\sqrt 3 \) (cm).

Diện tích tam giác ABC là: \(\frac{1}{2}AH \cdot BC = \frac{1}{2} \cdot 2\sqrt 3 \cdot 4 = 4\sqrt 3 \) (cm²).