Cho tam giác ABC vuông tại đỉnh A, có BC = 26 cm và AB/AC = 5/12. Tính độ dài các cạnh AB, AC.

Trả lời

Lời giải

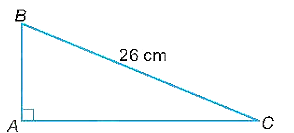
Xét tam giác ABC vuông tại A.

Áp dụng định lí Pythagore ta có:

AB² + AC² = BC² (1)

Mà $\frac{{AB}}{{AC}} = \frac{5}{{12}}$ nên AB = $\frac{5}{{12}}$AC, thay vào (1) ta có:

$A{C^2} + {\left( {\frac{5}{{12}}AC} \right)^2} = {26^2}$

$\frac{{169}}{{144}}A{C^2} = 676$

AC² = 576

Suy ra AC = 24 cm.

Do đó, AB = $\frac{5}{{12}}$.24 = 10 (cm).