Cho tam giác ABC vuông tại đỉnh A. Gọi AD là đường cao của tam giác. Biết rằng BD = 2 cm, CD = 8 cm. Hãy tính độ dài các cạnh AB, AC và chiều cao AD của tam giác ABC.

Trả lời

Lời giải

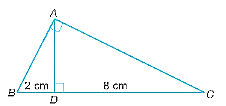
Vì AD là đường cao của tam giác ABC nên AD vuông góc với BC.

Do đó, \(\widehat {ADB} = \widehat {ADC} = 90^\circ \).

Tam giác ABD và tam giác CAD có:

\(\widehat {ADB} = \widehat {ADC} = 90^\circ \) (cmt)

\(\widehat {BAD} = \widehat C\) (cùng phụ với góc DAC).

Do đó, ∆ABD ᔕ ∆CAD (g.g).

Suy ra \(\frac{{AD}}{{CD}} = \frac{{BD}}{{AD}}\) nên AD² = CD . BD = 8 . 2 = 16.

Do đó, AD = 4 cm.

Áp dụng định lý Pythagore trong tam giác vuông ABD vuông tại D có:

AB² = AD² + BD² = 4² + 2² = 20.

Nên AB = \(2\sqrt 5 \)cm.

Áp dụng định lý Pythagore vào tam giác ACD vuông tại D có:

AC² = AD² + CD² = 4² + 8² = 80.

Nên AC = \(4\sqrt 5 \) cm.