Cho tam giác ABC vuông cân tại đỉnh A có đường cao AH. Biết rằng AB = 4 cm, hãy tính độ dài cạnh đáy BC và chiều cao AH.

Trả lời

Lời giải

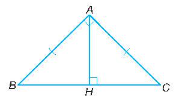
Vì tam giác ABC vuông cân tại A nên

AC = AB = 4 cm

\(\widehat B = \widehat C = 45^\circ \)

Tam giác AHB vuông tại H có \(\widehat B = 45^\circ \), suy ra tam giác AHB vuông cân tại H.

Nên AH = HB.

Tam giác AHC vuông tại H có \(\widehat C = 45^\circ \), suy ra tam giác AHC vuông cân tại H.

Nên AH = HC.

Khi đó, HB = HC = AH.

Mà HB + HC = BC. Suy ra HB + HB = BC hay 2HB = BC.

Do đó, AH = HC = HB = \(\frac{1}{2}\)BC.

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = 4² + 4² = 32.

Suy ra BC = \(\sqrt {32} \) = \(4\sqrt 2 \) (cm).

Do đó, AH = \(\frac{1}{2}\)BC = \(2\sqrt 2 \) (cm).