Tam giác ABC có cạnh BC dài nhất. Chứng minh số đo góc A lớn hơn hoặc bằng 60°

Bài 9.1 trang 48 SBT Toán 7 Tập 2: Tam giác ABC có cạnh BC dài nhất. Chứng minh số đo góc A lớn hơn hoặc bằng 60°.

Trả lời

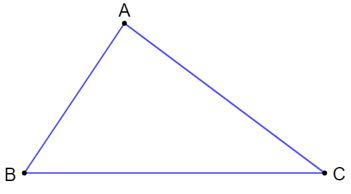
Xét tam giác ABC có BC là cạnh dài nhất và góc đối diện của cạnh BC là $\widehat{A}$  nên theo định lí 1 ta có $\widehat{A}$  là góc lớn nhất thỏa mãn: $\widehat{A}\ge \widehat{B},\widehat{A}\ge \widehat{C}$ .

Suy ra $\widehat{A}+\widehat{A}+\widehat{A}\ge \widehat{A}+\widehat{B}+\widehat{C}$

Hay $3\widehat{A}\ge \widehat{A}+\widehat{B}+\widehat{C}$

Do đó $\widehat{A}\ge \frac{\widehat{A}+\widehat{B}+\widehat{C}}{3}$ .

Mà tổng ba góc trong một tam giác là 180º.

Nên $\widehat{A}+\widehat{B}+\widehat{C}=180°$ .

Từ đó ta có: $\widehat{A}\ge \frac{\widehat{A}+\widehat{B}+\widehat{C}}{3}=\frac{180°}{3}=60°$ .

Vậy suy ra số đo góc A lớn hơn hoặc bằng 60º (đpcm).

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 30: Làm quen với xác suất của biến cố

Ôn tập chương 8

Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác

Bài 32: Quan hệ giữa đường vuông góc và đường xiên

Bài 33: Quan hệ giữa ba cạnh trong một tam giác

Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác