Bài 9.2 trang 48 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A, hai điểm D, E nằm trên đường thẳng BC, D nằm giữa B và C, C nằm giữa D và E. Chứng minh AD < AC < AE.
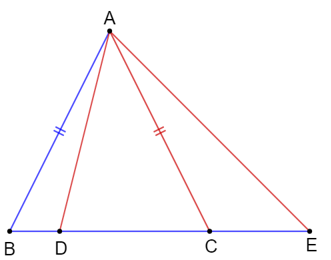
Do trong một tam giác cân, hai góc của đáy luôn bé hơn 90º nên suy ra là góc nhọn.
Mà kề bù với nên suy ra là góc tù.
Xét tam giác ACE có là góc tù nên cạnh đối diện với là cạnh AE là cạnh lớn nhất.
Suy ra AE > AC (*)
Mà tam giác ABC cân tại A nên AB = AC và .
Lại có:
Xét tam giác ABC có:
Suy ra (1)
Xét tam giác ABD có:
Suy ra (2)
Mà D nằm giữa B và C nên suy ra (3)
Từ (1), (2) và (3) ta suy ra:
Hay
Do đó .
Áp dụng định lí 2 ta được AB > AD
Mà AB = AC (cmt) nên suy ra AC > AD (**)
Từ (*) và (**) nên suy ra AE > AC > AD (đpcm).
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 30: Làm quen với xác suất của biến cố
Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác
Bài 32: Quan hệ giữa đường vuông góc và đường xiên
Bài 33: Quan hệ giữa ba cạnh trong một tam giác
Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác