Tam giác ABC có AD, BE là hai đường phân giác và . Chứng minh rằng DE là tia phân giác của góc ADC
Bài 9.17 trang 55 SBT Toán 7 Tập 2: Tam giác ABC có AD, BE là hai đường phân giác và . Chứng minh rằng DE là tia phân giác của góc ADC.
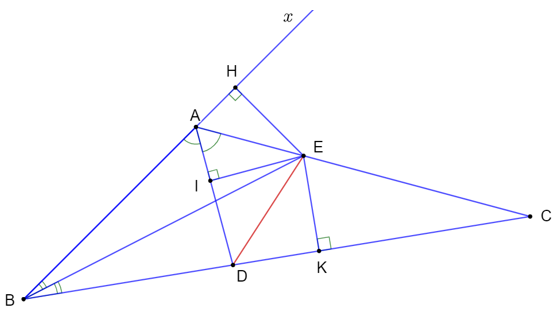
Gọi Ax là tia đối của tia AB thì ba góc BAD, DAC, CAx có cùng số đo 60º.
Hạ EH ⏊ Bx, EI ⏊ AD, EK ⏊ BC.
Ta có: Vì BE là phân giác góc ABC nên suy ra EH = EK (Áp dụng định lí 2).
Vì AE là phân giác góc DAx nên suy ra EH = EI (Áp dụng định lí 2).
Suy ra EK = EI hay E nằm trên tia phân giác của ADC.
Vậy suy ra DE là đường phân giác của góc ADC (đpcm).
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 32: Quan hệ giữa đường vuông góc và đường xiên
Bài 33: Quan hệ giữa ba cạnh trong một tam giác
Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác