Câu hỏi:
21/12/2023 62
Một xưởng sản xuất sử dụng ba loại máy để sản xuất hai loại sản phẩm quần và áo. Để sản xuất 1 cái áo lãi 200 nghìn đồng người ta sử dụng máy I trong 1 giờ, máy II trong 2 giờ và máy III trong 3 giờ. Để sản xuất 1 cái quần lãi 300 nghìn đồng người ta sử dụng máy I trong 3 giờ, máy II trong 4 giờ mà máy III trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 50 giờ, máy II hoạt động không quá 70 giờ và máy III hoạt động không quá 48 giờ. Hỏi phải sản xuất bao nhiêu quần và áo để xưởng sản xuất đạt mức lãi cao nhất ?
Một xưởng sản xuất sử dụng ba loại máy để sản xuất hai loại sản phẩm quần và áo. Để sản xuất 1 cái áo lãi 200 nghìn đồng người ta sử dụng máy I trong 1 giờ, máy II trong 2 giờ và máy III trong 3 giờ. Để sản xuất 1 cái quần lãi 300 nghìn đồng người ta sử dụng máy I trong 3 giờ, máy II trong 4 giờ mà máy III trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 50 giờ, máy II hoạt động không quá 70 giờ và máy III hoạt động không quá 48 giờ. Hỏi phải sản xuất bao nhiêu quần và áo để xưởng sản xuất đạt mức lãi cao nhất ?
A. 5 cái áo và 15 cái quần;
A. 5 cái áo và 15 cái quần;
B. 10 cái áo và 15 cái quần;
C. 12 cái áo và 13 cái quần;
D. 10 cái áo và 10 cái quần.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Gọi x, y (cái) lần lượt là số áo và số quần mà xưởng cần sản xuất (x, y ∈ ℕ).
Khi đó ta có:
x + 3y (giờ) là thời gian hoạt động của máy I;
2x + 4y (giờ) là thời gian hoạt động của máy II;
3x + 2y (giờ) là thời gian hoạt động của máy III.
Số tiền lãi của nhà máy L = 200x + 300y (nghìn đồng).
Do máy I chỉ hoạt động không quá 50 giờ, máy II hoạt động không quá 70 giờ và máy III hoạt động không quá 48 giờ nên ta có hệ .
Khi đó bài toán trở thành tìm số tự nhiên x, y thỏa hệ để L = 200x + 300y đạt giá trị lớn nhất.
Ta biểu diễn miền nghiệm của hệ với x ≥ 0; y ≥ 0.
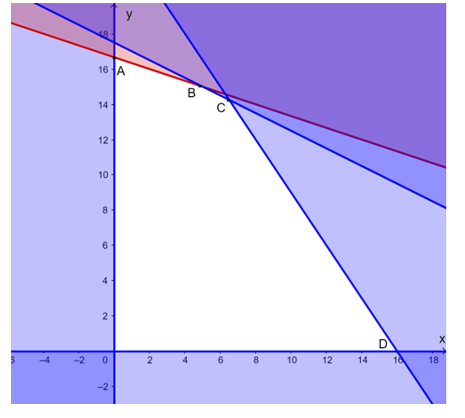
Miền nghiệm của hệ là miền ngũ giác OABCD (kể cả biên) với O(0; 0), , B(5; 15), , D(16; 0).
L lớn nhất tại các đỉnh của ngũ giác OABCD, do x, y ∈ ℕ nên ta chỉ cần tính giá trị của L tại các đỉnh O, B, D và so sánh.
Ta có:
L(0; 0) = 0, L(5; 15) = 5500, L(16; 0) = 3200.
Do đó, Lmax = 5500 tại x = 5 và y = 15.
Vậy phải sản xuất 5 cái áo và 15 cái quần để lợi nhuận lớn nhất.
Hướng dẫn giải
Đáp án đúng là: A
Gọi x, y (cái) lần lượt là số áo và số quần mà xưởng cần sản xuất (x, y ∈ ℕ).
Khi đó ta có:
x + 3y (giờ) là thời gian hoạt động của máy I;
2x + 4y (giờ) là thời gian hoạt động của máy II;
3x + 2y (giờ) là thời gian hoạt động của máy III.
Số tiền lãi của nhà máy L = 200x + 300y (nghìn đồng).
Do máy I chỉ hoạt động không quá 50 giờ, máy II hoạt động không quá 70 giờ và máy III hoạt động không quá 48 giờ nên ta có hệ .
Khi đó bài toán trở thành tìm số tự nhiên x, y thỏa hệ để L = 200x + 300y đạt giá trị lớn nhất.
Ta biểu diễn miền nghiệm của hệ với x ≥ 0; y ≥ 0.

Miền nghiệm của hệ là miền ngũ giác OABCD (kể cả biên) với O(0; 0), , B(5; 15), , D(16; 0).
L lớn nhất tại các đỉnh của ngũ giác OABCD, do x, y ∈ ℕ nên ta chỉ cần tính giá trị của L tại các đỉnh O, B, D và so sánh.
Ta có:
L(0; 0) = 0, L(5; 15) = 5500, L(16; 0) = 3200.
Do đó, Lmax = 5500 tại x = 5 và y = 15.
Vậy phải sản xuất 5 cái áo và 15 cái quần để lợi nhuận lớn nhất.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một xưởng sản xuất 2 món đồ chơi :
- Mỗi món đồ chơi loại I cần 1 kg nguyên liệu và 20 giờ làm, đem lại mức lời 30 nghìn đồng.
- Mỗi món đồ chơi loại II cần 2 kg nguyên liệu và 27 giờ làm, đem lại mức lời 50 nghìn đồng.
Biết xưởng có 140 kg nguyên liệu và 2150 giờ làm. Nên sản xuất mỗi loại đồ chơi là bao nhiêu để đem lại mức lời cao nhất ?
Một xưởng sản xuất 2 món đồ chơi :
- Mỗi món đồ chơi loại I cần 1 kg nguyên liệu và 20 giờ làm, đem lại mức lời 30 nghìn đồng.
- Mỗi món đồ chơi loại II cần 2 kg nguyên liệu và 27 giờ làm, đem lại mức lời 50 nghìn đồng.
Biết xưởng có 140 kg nguyên liệu và 2150 giờ làm. Nên sản xuất mỗi loại đồ chơi là bao nhiêu để đem lại mức lời cao nhất ?
Câu 2:
Cho hệ . Gọi S1 là tập nghiệm của bất phương trình (1), S2 là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì
Cho hệ . Gọi S1 là tập nghiệm của bất phương trình (1), S2 là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì
Câu 3:
Giá trị nhỏ nhất của biểu thức F(x; y) = 3y − 2x trên miền xác định bởi hệ là :
Giá trị nhỏ nhất của biểu thức F(x; y) = 3y − 2x trên miền xác định bởi hệ là :
Câu 4:
Giá trị lớn nhất của biểu thức G(x; y) = 10x + 20y trên miền xác định bởi hệ là :
Giá trị lớn nhất của biểu thức G(x; y) = 10x + 20y trên miền xác định bởi hệ là :


