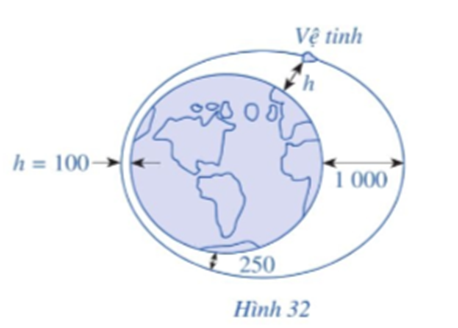
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
• Để vệ tinh cách mặt đất 1 000 km thì \(550 + 450\cos \frac{\pi }{{50}}t = 1\,\,\,000\)
\( \Leftrightarrow 450\cos \frac{\pi }{{50}}t = 450\)
\( \Leftrightarrow \cos \frac{\pi }{{50}}t = 1\)
\( \Leftrightarrow \frac{\pi }{{50}}t = k2\pi \,\,\,\left( {k \in \mathbb{Z},\,t \ge 0} \right)\)
\[ \Leftrightarrow t = k2\pi .\frac{{50}}{\pi } = 100k\,\,\left( {k \in \left\{ {0;1;2;3;...} \right\}} \right)\]
Vậy tại các thời điểm t = 100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 1 000 km.
• Để vệ tinh cách mặt đất 250 km thì \(550 + 450\cos \frac{\pi }{{50}}t = 250\)
\( \Leftrightarrow 450\cos \frac{\pi }{{50}}t = - 300\)
\( \Leftrightarrow \cos \frac{\pi }{{50}}t = - \frac{2}{3}\)
\[ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{{50}}t \approx 2,3 + k2\pi \\\frac{\pi }{{50}}t \approx - 2,3 + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}\,,\,\,t \ge 0} \right)\]
(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp ta được kết quả gần đúng là 2,3)
\[ \Leftrightarrow \left[ \begin{array}{l}t \approx \frac{{115}}{\pi } + 100k\\t \approx - \frac{{115}}{\pi } + 100k\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}\,,\,\,t \ge 0} \right)\]
Vậy tại các thời điểm \[t \approx \pm \frac{{115}}{\pi } + 100k\](với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 250 km.
• Để vệ tinh cách mặt đất 100 km thì \(550 + 450\cos \frac{\pi }{{50}}t = 1\,00\)
\( \Leftrightarrow 450\cos \frac{\pi }{{50}}t = - 450\)
\( \Leftrightarrow \cos \frac{\pi }{{50}}t = - 1\)
\( \Leftrightarrow \frac{\pi }{{50}}t = \pi + k2\pi \,\,\,\left( {k \in \mathbb{Z},\,t \ge 0} \right)\).
\( \Leftrightarrow t = 50 + 100k\,\,\,\left( {k \in \left\{ {0;1;2;3;...} \right\}} \right)\).
Vậy tại các thời điểm t = 50 + 100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 100 km.