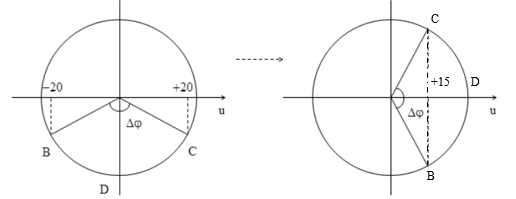
Một sóng cơ lan truyền trên sợi dây từ B đến C với chu kì T = 2s, biên độ
Một sóng cơ lan truyền trên sợi dây từ \({\rm{B}}\) đến \({\rm{C}}\) với chu kì \({\rm{T}} = 2{\rm{\;s}}\), biên độ không đổi. Ở thời điểm \({{\rm{t}}_0}\), li độ các phần tử tại \({\rm{B}}\) và \({\rm{C}}\) tương ứng là \( - 20{\rm{\;mm}}\) và \( + 20{\rm{\;mm}}\); phần tử tại trung điểm \({\rm{D}}\) của \({\rm{BC}}\) đang ở vị trí cân bằng. Ở thời điểm \({{\rm{t}}_1}\), li độ các phần tử tại \({\rm{B}}\) và \({\rm{C}}\) cùng là \( + 15{\rm{\;mm}}\). Tại thời điểm \({{\rm{t}}_2} = {{\rm{t}}_1} + 0,25{\rm{\;s}}\) li độ của phần tử \({\rm{D}}\) có độ lớn gần nhất với giá trị nào sau đây?
A. \(17,32{\rm{\;mm}}\).
B. \(14,14{\rm{\;mm}}\).
C. \(21,65{\rm{\;mm}}\).
D. \(17,67{\rm{\;mm}}\).
