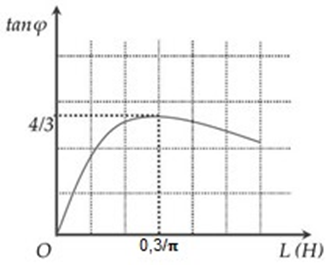
Mạch điện xoay chiêu AB gồm AM, MN và NB ghép nối tiếp, \({\rm{AM}}\) chứa điện trở \({\rm{R}},{\rm{MN}}\) chứa cuộn dây có điện trở \({\rm{r}}\) và độ tự cảm \({\rm{L}}\) thay đổi được, \({\rm{NB}}\) chứa tụ có điện dung C. Đặt điện áp xoay chiều \({\rm{u}} = 220\sqrt 2 {\rm{cos}}100{\rm{\pi t\;}}\left( {\rm{V}} \right)\) vào hai đầu mạch điện. Gọi \({\rm{\varphi }}\) là góc lệch pha giữa u_MN và u_AN, đồ thị biểu diễn \({\rm{tan\varphi }}\) theo L như hình vẽ. Khi \({\rm{\varphi }}\) đạt cực đại thì điện áp hiệu dụng của đoạn \({\rm{MB}}\) đạt cực tiểu. Khi điện áp hiệu dụng giữa hai đầu cuộn dây bằng \(220{\rm{\;V}}\) thì công suất tiêu thụ của cuộn dây bằng

\({U_{MB\min }} \Rightarrow \)cộng hưởng \( \Rightarrow {Z_C} = {Z_L} = \omega L = 100\pi .0,3/\pi = 30\Omega \)

\(\tan \left( {{\varphi _{MN}} - {\varphi _{AN}}} \right) = \frac{{\tan {\varphi _{MN}} - \tan {\varphi _{AN}}}}{{1 + \tan {\varphi _{MN}}\tan {\varphi _{AN}}}} = \frac{{\frac{{{Z_L}}}{r} - \frac{{{Z_L}}}{{R + r}}}}{{1 + \frac{{{Z_L}}}{r}.\frac{{{Z_L}}}{{R + r}}}} = \frac{R}{{\frac{{r\left( {R + r} \right)}}{{{Z_L}}} + {Z_L}}}\mathop \le \limits_{{\mathop{\rm Cos}\nolimits} i} \frac{R}{{2\sqrt {r\left( {R + r} \right)} }}\)

\( \Rightarrow \frac{4}{3} = \frac{R}{{2\sqrt {r\left( {R + r} \right)} }}\) (1) xảy ra khi \(\frac{{r\left( {R + r} \right)}}{{{Z_L}}} = {Z_L} \Rightarrow \sqrt {r\left( {R + r} \right)} = {Z_L} = 30\) (2)

Từ (1) và (2) \( \Rightarrow R = 80 \to r = 10\)

Khi \({U_{rL}} = \frac{{U\sqrt {{r^2} + Z_L^2} }}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} \Rightarrow 220 = \frac{{220\sqrt {{{10}^2} + Z_L^2} }}{{\sqrt {{{\left( {80 + 10} \right)}^2} + {{\left( {{Z_L} - 30} \right)}^2}} }} \Rightarrow {Z_L} = \frac{{445}}{3}\)

\({P_{rL}} = \frac{{{U^2}r}}{{{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} = \frac{{{{220}^2}.10}}{{{{\left( {80 + 10} \right)}^2} + {{\left( {\frac{{445}}{3} - 30} \right)}^2}}} \approx 21,9W\). Chọn C