Câu hỏi:
19/12/2023 71
Một phân xưởng có hai máy đặc chủng loại 1 và loại 2 sản xuất hai loại sản phẩm kí hiệu là A và B. Một tấn sản phẩm loại A lãi 2 triệu đồng, một tấn sản phẩm loại B lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A phải dùng máy loại 1 trong 3 giờ và máy loại 2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B phải dùng máy loại 1 trong 1 giờ và máy loại 2 trong 1 giờ. Máy loại 1 làm việc không quá 6 giờ một ngày, máy loại 2 làm việc không quá 4 giờ 1 ngày. Hỏi cần sản xuất bao nhiêu tấn sản phẩm loại A và loại B để số tiền lãi mà phân xưởng này có thể thu được trong một ngày là lớn nhất?
Một phân xưởng có hai máy đặc chủng loại 1 và loại 2 sản xuất hai loại sản phẩm kí hiệu là A và B. Một tấn sản phẩm loại A lãi 2 triệu đồng, một tấn sản phẩm loại B lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A phải dùng máy loại 1 trong 3 giờ và máy loại 2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B phải dùng máy loại 1 trong 1 giờ và máy loại 2 trong 1 giờ. Máy loại 1 làm việc không quá 6 giờ một ngày, máy loại 2 làm việc không quá 4 giờ 1 ngày. Hỏi cần sản xuất bao nhiêu tấn sản phẩm loại A và loại B để số tiền lãi mà phân xưởng này có thể thu được trong một ngày là lớn nhất?
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi x, y lần lượt là số tấn sản phẩm loại A, B mà phân xưởng sản xuất trong 1 ngày (x ≥ 0, y ≥ 0).
Khi đó, số tiền lãi một ngày là: F(x; y) = 2x + 1,6y (triệu đồng).
Số giờ làm việc trong ngày của máy loại 1 là 3x + y.
Số giờ làm việc trong ngày của máy loại 2 là x + y.
Vì máy loại 1 làm việc không quá 6 giờ một ngày, máy loại 2 làm việc không quá 4 giờ 1 ngày nên ta có hệ bất phương trình .
Miền nghiệm của hệ bất phương trình là miền tứ giác OABC không bị gạch trong hình vẽ.
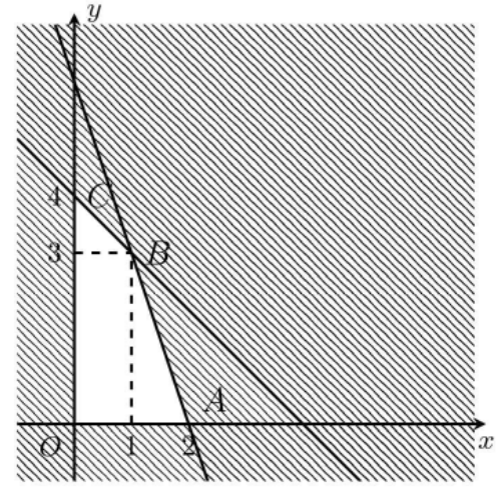
Ta có:
F(0; 0) = 2 . 0 + 1,6 . 0 = 0;
F(2; 0) = 2 . 2 + 1,6 . 0 = 4;
F(1; 3) = 2 . 1 + 1,6 . 3 = 6,8;
F(0; 4) = 2 . 0 + 1,6 . 4 = 6,4.
Do đó F(x; y) lớn nhất bằng 6,8 khi (x; y) = (1; 3).
Vậy để thu được lãi lớn nhất phải sản xuất 1 tấn sản phẩm loại A và 3 tấn sản phẩm loại B.
Gọi x, y lần lượt là số tấn sản phẩm loại A, B mà phân xưởng sản xuất trong 1 ngày (x ≥ 0, y ≥ 0).
Khi đó, số tiền lãi một ngày là: F(x; y) = 2x + 1,6y (triệu đồng).
Số giờ làm việc trong ngày của máy loại 1 là 3x + y.
Số giờ làm việc trong ngày của máy loại 2 là x + y.
Vì máy loại 1 làm việc không quá 6 giờ một ngày, máy loại 2 làm việc không quá 4 giờ 1 ngày nên ta có hệ bất phương trình .
Miền nghiệm của hệ bất phương trình là miền tứ giác OABC không bị gạch trong hình vẽ.

Ta có:
F(0; 0) = 2 . 0 + 1,6 . 0 = 0;
F(2; 0) = 2 . 2 + 1,6 . 0 = 4;
F(1; 3) = 2 . 1 + 1,6 . 3 = 6,8;
F(0; 4) = 2 . 0 + 1,6 . 4 = 6,4.
Do đó F(x; y) lớn nhất bằng 6,8 khi (x; y) = (1; 3).
Vậy để thu được lãi lớn nhất phải sản xuất 1 tấn sản phẩm loại A và 3 tấn sản phẩm loại B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho định lý sau: “Nếu hai tam giác bằng nhau thì hai tam giác đó đồng dạng”.
Phát biểu định lý trên dưới dạng điều kiện cần.
Cho định lý sau: “Nếu hai tam giác bằng nhau thì hai tam giác đó đồng dạng”.
Phát biểu định lý trên dưới dạng điều kiện cần.
Câu 4:
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?
Câu 5:
Tam giác ABC có BC = 6, AC = 7, AB = 8. Bán kính đường tròn nội tiếp của tam giác ABC là
Tam giác ABC có BC = 6, AC = 7, AB = 8. Bán kính đường tròn nội tiếp của tam giác ABC là
Câu 8:
Cho các mệnh đề dưới đây:
(1) 24 là số nguyên tố.
(2) Phương trình x2 – 5x + 9 = 0 có 2 nghiệm thực phân biệt.
(3) Phương trình x2 + 1 = 0 có 2 nghiệm thực phân biệt.
(4) Mọi số nguyên lẻ đều không chia hết cho 2.
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?
Cho các mệnh đề dưới đây:
(1) 24 là số nguyên tố.
(2) Phương trình x2 – 5x + 9 = 0 có 2 nghiệm thực phân biệt.
(3) Phương trình x2 + 1 = 0 có 2 nghiệm thực phân biệt.
(4) Mọi số nguyên lẻ đều không chia hết cho 2.
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?
Câu 9:
Cho tam giác ABC có AB = 4, AC = 8 và . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
Cho tam giác ABC có AB = 4, AC = 8 và . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
Câu 11:
Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 3x + 2y < 10?
Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 3x + 2y < 10?
Câu 13:
Để xác định chiều cao của một tòa tháp mà không cần lên đỉnh của tòa nhà người ta làm như sau: đặt giác kế thẳng đứng cách chân tháp một khoảng AB = 55 m, chiều cao của giác kế là OA = 2 m.
Quay thanh giác kế sao cho khi ngắm theo thanh ta nhìn thấy đỉnh C của tháp. Đọc trên giác kế số đo góc COD=60.
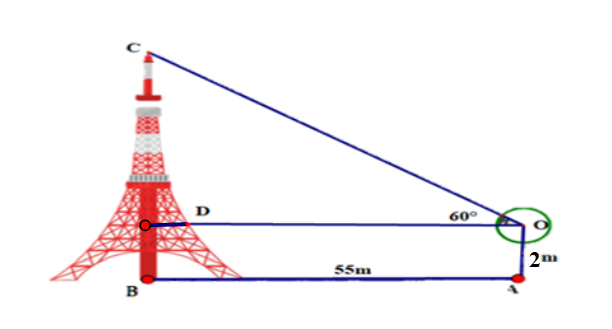
Chiều cao của ngọn tháo gần nhất với giá trị nào sau đây?
Để xác định chiều cao của một tòa tháp mà không cần lên đỉnh của tòa nhà người ta làm như sau: đặt giác kế thẳng đứng cách chân tháp một khoảng AB = 55 m, chiều cao của giác kế là OA = 2 m.
Quay thanh giác kế sao cho khi ngắm theo thanh ta nhìn thấy đỉnh C của tháp. Đọc trên giác kế số đo góc COD=60.

Chiều cao của ngọn tháo gần nhất với giá trị nào sau đây?
Câu 14:
Miền nghiệm của hệ bất phương trình là phần màu trắng được biểu diễn trong hình vẽ nào dưới dây ?
Miền nghiệm của hệ bất phương trình là phần màu trắng được biểu diễn trong hình vẽ nào dưới dây ?
Câu 15:
Cho tam giác ABC có b = 7; c = 5, cosA =. Độ dài đường cao ha của tam giác ABC là
Cho tam giác ABC có b = 7; c = 5, cosA =. Độ dài đường cao ha của tam giác ABC là


