Quan sát Hình 21 và cho biết dấu của tam thức bậc hai f(x) = x^2 + 3x + 2 tùy theo các khoảng của x
524
07/06/2023
Hoạt động 3 trang 45 Toán lớp 10 Tập 1:
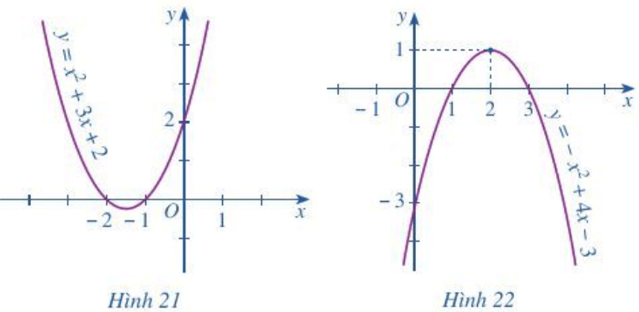
a) Quan sát Hình 21 và cho biết dấu của tam thức bậc hai f(x) = x2 + 3x + 2 tùy theo các khoảng của x.
b) Quan sát Hình 22 và cho biết dấu của tam thức bậc hai f(x) = – x2 + 4x – 3 tùy theo các khoảng của x.
c) Từ đó rút ra mối quan hệ về dấu của tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0) với dấu của hệ số a tùy theo các khoảng của x trong trường hợp ∆ > 0.
Trả lời
a) Quan sát Hình 21, ta thấy:
Parabol f(x) = x2 – 2x + 2 cắt trục hoành tại hai điểm phân biệt x = -2 và x = -1.
+ Trên khoảng (– 2; – 1), phần parabol nằm hoàn toàn phía dưới trục hoành nên trong khoảng này tam thức bậc hai f(x) = x2 + 3x + 2 < 0.
+ Trên các khoảng (– ∞; – 2) và (– 1; + ∞), phần parabol nằm hoàn toàn phía trên trục hoành nên trong khoảng này tam thức bậc hai f(x) = x2 + 3x + 2 > 0.
b) Quan sát Hình 22, ta thấy:
Parabol y = - x2 + 4x – 3 cắt trục hoành tại hai điểm phân biệt x = 1 và x = 3.
+ Trên khoảng (1; 3), phần parabol nằm hoàn toàn phía trên trục hoành nên trong khoảng này tam thức bậc hai f(x) = – x2 + 4x – 3 > 0.
+ Trên các khoảng (– ∞; 1) và (3; + ∞), phần parabol nằm hoàn toàn phía dưới trục hoành nên trong khoảng này tam thức bậc hai f(x) = – x2 + 4x – 3 < 0.
c) Nếu ∆ > 0 thì f(x) cùng dấu với hệ số a với mọi x thuộc các khoảng (– ∞; x1) và (x2; + ∞); f(x) trái dấu với hệ số a với mọi x thuộc khoảng (x1; x2), trong đó x1, x2 là hai nghiệm của f(x) và x1 < x2.
Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:
Bài 1: Hàm số và đồ thị
Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
Bài 3: Dấu của tam thức bậc hai
Bài 4: Bất phương trình bậc hai một ẩn
Bài 5: Hai dạng phương trình quy về phương trình bậc hai
Bài tập cuối chương 3

