Cho hàm số y = – x^2 + 2x + 3. a) Tìm tọa độ 5 điểm thuộc đồ thị hàm số trên có hoành độ lần lượt là – 1, 0, 1, 2, 3 rồi vẽ chúng trong mặt phẳng tọa độ Oxy
750
08/06/2023
Hoạt động 3 trang 40 Toán lớp 10 Tập 1: Cho hàm số y = – x2 + 2x + 3.
a) Tìm tọa độ 5 điểm thuộc đồ thị hàm số trên có hoành độ lần lượt là – 1, 0, 1, 2, 3 rồi vẽ chúng trong mặt phẳng tọa độ Oxy.
b) Vẽ đường cong đi qua 5 điểm trên. Đường cong đó cũng là đường parabol và là đồ thị của hàm số y = – x2 + 2x + 3 (Hình 12).
c) Cho biết tọa độ của điểm cao nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
Trả lời
a)
Thay x = – 1 vào đồ thị hàm số đã cho ta được: y = – (– 1)2 + 2 . (– 1) + 3 = 0.
Thay x = 0 vào đồ thị hàm số đã cho ta được: y = – 02 + 2 . 0 + 3 = 3.
Thay x = 1 vào đồ thị hàm số đã cho ta được: y = – 12 + 2 . 1 + 3 = 4.
Thay x = 2 vào đố thị hàm số đã cho ta được: y = – 22 + 2 . 2 + 3 = 3.
Thay x = 3 vào đồ thị hàm số đã cho ta được: y = – 32 + 2 . 3 + 3 = 0.
Vậy tọa độ các điểm cần tìm là: A(– 1; 0), B(0; 3), C(1; 4), D(2; 3), E(3; 0) và được vẽ lên mặt phẳng tọa độ như sau:
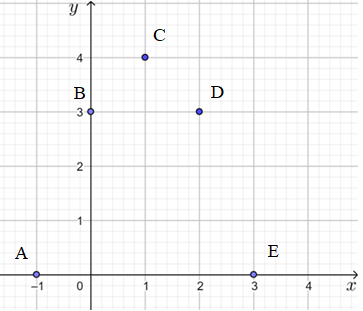
b) Vẽ đường cong đi qua 5 điểm trên:
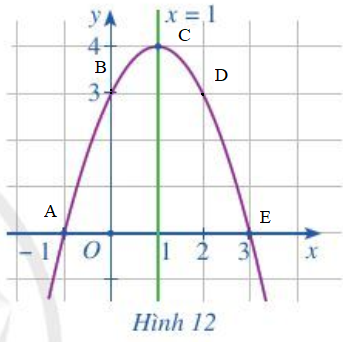
c) Tọa độ điểm cao nhất là (1; 4).
Phương trình trục đối xứng của parabol là: x = 1.
Đồ thị hàm số đó quay bề lõm hướng xuống dưới.
Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:
Bài tập cuối chương 2
Bài 1: Hàm số và đồ thị
Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
Bài 3: Dấu của tam thức bậc hai
Bài 4: Bất phương trình bậc hai một ẩn
Bài 5: Hai dạng phương trình quy về phương trình bậc hai


