Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng

Bài 9.43 trang 110 Toán 8 Tập 2:Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng.

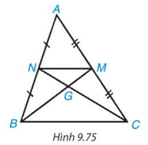
Trả lời

Vì BM, CN là các đường trung tuyến của tam giác ABC nên M, N lần lượt là trung điểm của AC, AB.

Suy ra MN là đường trung bình của tam giác ABC.

Do đó, MN // BC.

Suy ra $\widehat{GMN}=\widehat{GBC}$(hai góc ở vị trí so le trong).

Mặt khác $\widehat{NGM}=\widehat{CGB}$ (hai góc đối đỉnh).

Do đó, ∆GMN ∽ ∆GBC (g.g).

Vì MN là đường trung bình của tam giác ABC nên BC = 2MN.  

Khi đó, $\frac{GN}{GC}=\frac{GM}{GB}=\frac{MN}{BC}=\frac{1}{2}$ .

Vậy ∆GMN ∽ ∆GBC với tỉ số đồng dạng bằng $\frac{1}{2}$.

Xem thêm lời giải bài tập SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác: