Giải SGK Toán 8 (Kết nối tri thức) Luyện tập chung trang 121 Tập 2

Giải SGK Toán lớp 8 Luyện tập chung trang 121 Tập 2

Bài tập

Bài 10.11 trang 121 Toán 8 Tập 2: Tính thể tích của hình chóp tam giác đều S.ABC, biết diện tích đáy của nó bằng 15,6 cm2, chiều cao bằng 10 cm

Lời giải:

Thể tích của khối chóp tam giác đều S.ABC là

$V=\frac{1}{3}S\cdot h=\frac{1}{3}\cdot \mathrm{15,6}\cdot 10=52$ (cm³).

Bài 10.12 trang 122 Toán 8 Tập 2: Trong các miếng bìa ở Hình 10.32, miếng bìa nào khi gấp và dán lại thì được một hình chóp tam giác đều, miếng nào thì được một hình chóp tứ giác đều.

Lời giải:

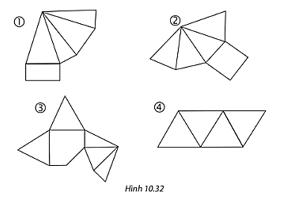
Miếng bìa 4 gấp và dán lại được hình chóp tam giác đều.

Miếng bìa 2 gấp và dán lại được hình chóp tứ giác đều.

Miếng bìa 1 và miếng bìa 3 không không có đáy là hình vuông hay hình tam giác nên không thỏa mãn.

Bài 10.13 trang 122 Toán 8 Tập 2: Tính thể tích hình chóp tam giác đều A.BCD có độ dài cạnh đáy bằng 10 cm, chiều cao bằng 12 cm (H.10.33), biết  $\sqrt{75}\approx \mathrm{8,66}$

Lời giải:

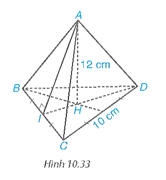
Vì I là trung điểm của BC nên BI = IC = 10 : 2 = 5 cm.

Xét tam giác BID vuông tại I, có

ID² + BI² = BD² (định lí Pythagore).

Suy ra ID² = BD² – BI² = 10² – 5² = 75.

Do đó, ID = $\sqrt{75}\approx \mathrm{8,66}$(cm).

Diện tích tam giác đáy BCD là:

S_BCD =  $\frac{1}{2}$. ID . BC ≈ $\frac{1}{2}$  . 8,66 . 10 = 43,3 (cm²).

Thể tích hình chóp tam giác đều A.BCD là: 

V = $\frac{1}{3}$  . S . h ≈$\frac{1}{3}$ . 43,3 . 12 = 173,2 (cm³).

Bài 10.14 trang 122 Toán 8 Tập 2: Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m.

a) Tính thể tích hình chóp. 

b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này, biết rằng người ta đo được độ dài cạnh bên của hình chóp là 31,92 m.

Lời giải:

a) Thể tích hình chóp tứ giác đều là:

V =  $\frac{1}{3}$. S_đáy . h = $\frac{1}{3}$  . 34² . 21 = 8 092 (cm³).

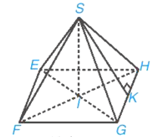
b) Mô tả hình chóp như hình dưới đây.

Ta có SI = 21 m, EF = FG = GH = HE = 34 m, SE = SF = SG = SH = 31,92 m.

SK là một trung đoạn của hình chóp.

K là trung điểm của GH nên GK = KH = $\frac{GH}{2}=\frac{34}{2}=17$  m.

Áp dụng định lí Pythagore cho tam giác SKH vuông tại H, ta có:

KH² + SK² = SH²

Hay 17² + SK² = (31,92)²

Suy ra SK² = (31,92)² – 17² ≈ 729,89. Do đó, SK ≈ 27,02 m.

Diện tích xung quanh của hình chóp tứ giác đều hay tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này là:

S_xq = p . d ≈ $\frac{34\cdot 4}{2}\cdot \mathrm{27,02}$ = 1 837,36 (m²).

Xem thêm lời giải bài tập SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác: