Gọi Ou và Ov lần lượt là hai tia phân giác của hai góc kề bù xOy và x’Oy; A là một điểm khác O trên tia Ox

Bài 3.37 trang 73 Toán 8 Tập 1: Gọi Ou và Ov lần lượt là hai tia phân giác của hai góc kề bù xOy và x’Oy; A là một điểm khác O trên tia Ox. Gọi B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov. Hỏi tứ giác OBAC là hình gì? Vì sao?

Trả lời

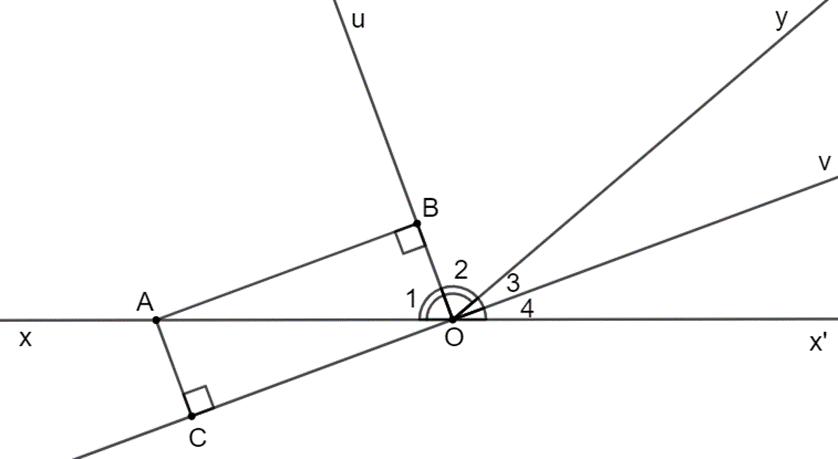
Vì Ou, Ov lần lượt là tia phân giác của $\widehat{xOy};\widehat{x^{\text{'}}Oy}$ nên ${\hat{O}}_1={\hat{O}}_2;{\hat{O}}_3={\hat{O}}_4$ .

Mà $\widehat{xOy}+\widehat{x^{\text{'}}Oy}=180°$ (vì $\widehat{xOy};\widehat{x^{\text{'}}Oy}$ là hai góc kề bù).

Hay ${\hat{O}}_1+{\hat{O}}_2+{\hat{O}}_3+{\hat{O}}_4=180°$

Suy ra $2{\hat{O}}_2+2{\hat{O}}_3=180°$ .

Do đó ${\hat{O}}_2+{\hat{O}}_3=90°$ hay $\widehat{uOv}=90°$ suy ra $\widehat{uOC}=90°$ hay $\widehat{BOC}=90°$ .

Vì B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov

Nên $\widehat{ABO}=90°;\widehat{ACO}=90°$ .

Tứ giác OBAC có $\widehat{ACO}+\widehat{BOC}+\widehat{ABO}+\widehat{BAC}=360°$

$90°+90°+90°+\widehat{BAC}=360°$

$270°+\widehat{BAC}=360°$

Suy ra $\widehat{BAC}=360°-270°=90°$ .

Xét tứ giác OBAC có $\widehat{BOC}=90°$ ; $\widehat{ABO}=90°;\widehat{ACO}=90°$ ; $\widehat{BAC}=90°$ .

Vậy tứ giác OBAC là hình chữ nhật.

Xem thêm các bài giải SGK Toán 8 Kết nối tri thức hay, chi tiết khác: