Gọi H là giao của ba đường cao AI, BJ, CK của tam giác nhọn ABC

Bài 3.29 trang 44 SBT Toán 8 Tập 1: Gọi H là giao của ba đường cao AI, BJ, CK của tam giác nhọn ABC. Dùng công thức tính diện tích tam giác để chứng minh:

$\frac{HI}{AI}+\frac{HJ}{BJ}+\frac{HK}{CK}=1.$

Hỏi khi góc A của tam giác ABC là góc tù thì công thức đó thay đổi thế nào?

Trả lời

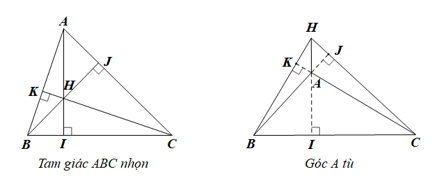
Kí hiệu S là diện tích tam giác.

• Xét trường hợp tam giác ABC nhọn, ta có

$S_{HBC}=\frac{1}{2}\cdot HI\cdot BC;$ $S_{ABC}=\frac{1}{2}\cdot AI\cdot BC$

Suy ra $\frac{S_{HBC}}{S_{ABC}}=\frac{\frac{1}{2}\cdot HI\cdot BC}{\frac{1}{2}\cdot AI\cdot BC}=\frac{HI}{AI}$

Chứng minh tương tự, ta có: $\frac{S_{HAC}}{S_{ABC}}=\frac{HJ}{BJ}$ và $\frac{S_{HAB}}{S_{ABC}}=\frac{HK}{CK}$.

Suy ra, $\frac{HI}{AI}+\frac{HJ}{BJ}+\frac{HK}{CK}=\frac{S_{HBC}+S_{HAC}+S_{HAB}}{S_{ABC}}$(do H nằm bên trong tam giác ABC)

Do đó $\frac{HI}{AI}+\frac{HJ}{BJ}+\frac{HK}{CK}=\frac{S_{ABC}}{S_{ABC}}=1$.

• Khi góc A là góc tù, H nằm trong góc đối đỉnh với góc BAC, ta có

S_ABC = S_HBC – S_HAB – S_HAC nên ta được $1=\frac{HI}{AI}-\frac{HJ}{BJ}-\frac{HK}{CK}$.

Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:

Bài 13: Hình chữ nhật

Bài 14: Hình thoi và hình vuông

Bài tập cuối chương 3

Bài 15: Định lí Thalès trong tam giác

Bài 16: Đường trung bình của tam giác

Bài 17: Tính chất đường phân giác của tam giác