Cho tam giác ABC. Với mỗi điểm M nằm giữa B và C, lấy điểm N thuộc cạnh AB, điểm P thuộc cạnh AC sao cho MN // AC
437
08/11/2023
Bài 3.28 trang 44 SBT Toán 8 Tập 1: Cho tam giác ABC. Với mỗi điểm M nằm giữa B và C, lấy điểm N thuộc cạnh AB, điểm P thuộc cạnh AC sao cho MN // AC, MP // AB.
a) Hỏi tứ giác ANMP là hình gì?
b) Hỏi M ở vị trí nào để tứ giác ANMP là một hình thoi?
c) Tam giác ABC phải thoả mãn điều kiện gì để tứ giác ANMP là một hình chữ nhật?
d) Khi tam giác ABC thoả mãn điều kiện nói trong câu c, tìm vị trí của M để NP ngắn nhất.
e) Tam giác ABC thoả mãn điều kiện gì và M ở vị trí nào trên cạnh BC để tứ giác ANMP là một hình vuông?
Trả lời
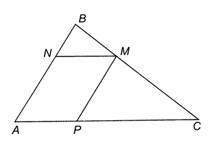
a) Ta có NM // AC hay MN // AP (do P ∈ BC)
MP // AB hay MP // AN (do N ∈ AB)
Tứ giác ANMP có MN // AP và MP // AN nên là hình bình hành.
b) Để ANMP là hình thoi thì tia AM phải là tia phân giác của góc A.
c) Để ANMP là hình chữ nhật thì hình bình hành ANMP phải có 1 góc vuông.
Khi đó thì góc A phải vuông tức là tam giác ABC vuông tại A.
d) Khi góc A là góc vuông, ANMP là hình chữ nhật nên AM = NP.
Vậy NP ngắn nhất khi AM ngắn nhất, lúc này AM là đường cao của tam giác ABC.
e) Tứ giác ANMP là hình vuông thì nó phải là hình chữ nhật và là hình thoi tức là tam giác ABC vuông tại A và có tia AM là phân giác của góc A.
Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:
Bài 13: Hình chữ nhật
Bài 14: Hình thoi và hình vuông
Bài tập cuối chương 3
Bài 15: Định lí Thalès trong tam giác
Bài 16: Đường trung bình của tam giác
Bài 17: Tính chất đường phân giác của tam giác

