Giải SBT Toán 8 (Kết nối tri thức) Bài 15: Định lí Thalès trong tam giác
Bài 4.1 trang 47 SBT Toán 8 Tập 1: Viết tỉ số của các cặp đoạn thẳng có độ dài như sau:
a) HK = 3 cm và MN = 9 cm;
b) AB = 36 cm và PQ = 12 dm;
c) EF = 1,5 m và GH = 30 cm.
Lời giải:
a) Ta có: HKMN=39=13.
b) Ta có: PQ = 12 dm = 120 cm.
Khi đó ABPQ=36120=310.
c) Ta có: EF = 1,5 m = 150 cm.
Khi đó EFGH=15030=5.
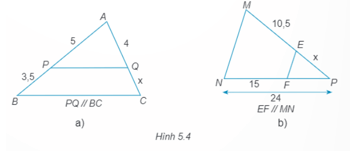
Bài 4.2 trang 48 SBT Toán 8 Tập 1: Tìm độ dài x trong các hình vẽ sau (H.5.4):
Lời giải:
a) Vì PQ // BC, theo Định lí Thalès ta có:
APPB=AQQC hay 53,5=4x. Suy ra x=4⋅3,55=2,8.
b) Ta có: FP = NP ‒ NF = 24 ‒15 = 9.
Vì EF // MN, theo Định lí Thalès ta có:
MEEP=NFFP hay 10,5x=159. Suy ra x=10,5⋅915=6,3
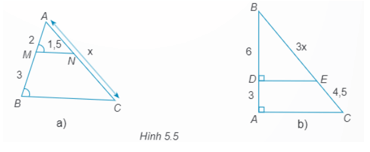
Bài 4.3 trang 48 SBT Toán 8 Tập 1: Tìm độ dài x trong Hình 5.5:
Lời giải:
a) Ta có ^AMN=^MBC(giả thiết), mà hai góc này ở vị tri đồng vị nên MN // BC.
Theo Định lí Thalès ta có: AMMB=ANNC hay 23=1,5NC
Suy ra NC=3⋅1,52=2,25.
Vậy x = AC = AN + NC = 1,5 + 2,25 = 3,75.
b) Ta có DE ⊥ AB và AC ⊥ AB nên DE // AC.
Theo Định lí Thalès, ta có: BDDA=BEEC hay 63=3x4,5
Suy ra x=6⋅4,59=3.
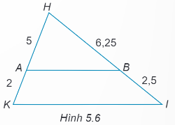
Bài 4.4 trang 48 SBT Toán 8 Tập 1: Cho Hình 5.6. Chứng minh rằng AB // KI.
Lời giải:
Ta có: HAAK=52; HBBI=6,252,5=52.
Suy ra HAAK=HBBI=52, theo Định lí Thalès đảo ta có: AB // KI.
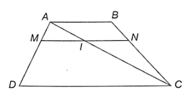
a) AMMD=BNNC;
b) AMAD+CNCB=1.
Lời giải:
a) Xét tam giác ADC, MI // DC nên theo định lí Thalès ta có: AMMD=AIIC.
Xét tam giác ABC, IN // AB nên theo định lí Thalès ta có: AIIC=BNNC.
Từ đó, suy ra AMMD=BNNC.
b) Xét tam giác ADC, MI // DC nên theo định lí Thalès ta có: AMAD=AIAC.
Xét tam giác ABC, IN // AB nên theo định lí Thalès ta có: CNCB=CICA.
Khi đó AMAD+CNCB=AIAC+CICA=AI+CICA=ACCA=1.
Lời giải:
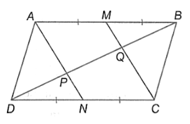
Do ABCD là hình bình hành nên AB // CD, AB = CD
Mà M, N lần lượt là trung điểm của AB và CD nên AM // NC và AM = NC
Tứ giác AMCN có AM // NC và AM = NC nên AMCN là hình bình hành.
Suy ra AN // MC.
Xét tam giác ABP, MQ // AP nên theo định lí Thalès ta có: BQQP=BMMA=1
Do đó BQ = QP. (1)
Xét tam giác DQC, PN // QC nên theo định lí Thalès ta có: DPPQ=DNNC=1
Do đó DP = PQ. (2)
Từ (1) và (2) suy ra BQ = QP = PD.
Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:
Bài 14: Hình thoi và hình vuông
Bài 16: Đường trung bình của tam giác