Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác. Chứng minh tổng các
28
18/08/2024
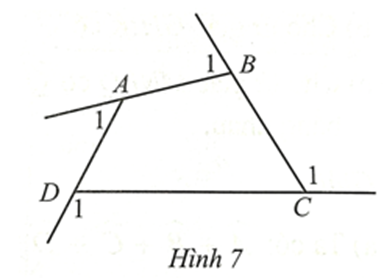
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác. Chứng minh tổng các góc ngoài của tứ giác ABCD ở Hình 7 (tại mỗi đỉnh chỉ chọn một góc ngoài): ˆA1+ˆB1+ˆC1+ˆD1=360∘.
Trả lời
Trong tứ giác ABCD, ta có: ^DAB+^ABC+^BCD+^CDA=360∘.
Ta có: ^DAB+^A1=^ABC+^B1=^BCD+^C1=^CDA+^D1=180∘ (các cặp góc kề bù).
Suy ra:
(180∘−^A1)+(180∘−^B1)+(180∘−^C1)+(180∘−^D1)=360∘
Hay 720∘−(^A1+^B1+^C1+^D1)=360∘.
Do đó ^A1+^B1+^C1+^D1=360∘.
Vậy ^A1+^B1+^C1+^D1=360∘.