Cho tứ giác MNPQ có PM là tia phân giác của góc NPQ, góc QMN = 110 độ
Cho tứ giác MNPQ có PM là tia phân giác của góc NPQ, ^QMN=110∘, ˆN=120∘, ˆQ=60∘ (Hình 8c). Tính số đo các góc NPM, MPQ, QMP.
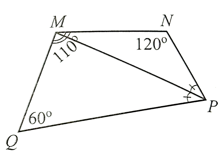
Cho tứ giác MNPQ có PM là tia phân giác của góc NPQ, ^QMN=110∘, ˆN=120∘, ˆQ=60∘ (Hình 8c). Tính số đo các góc NPM, MPQ, QMP.

Trong tứ giác MNPQ, ta có: ˆQ+^QMN+ˆN+^NPQ=360∘
Suy ra ^NPQ=360∘−(^QMN+ˆN+ˆQ)=360∘−(110∘+120∘+60∘)=70∘.
Do PM là tia phân giác của góc NPQ nên ta có:
^NPM=^MPQ=^NPQ2=70∘2=35∘.
Trong tam giác MPQ, ta có: ˆQ+^QMP+^MPQ=180∘
Suy ra ^QMP=180∘−(^MPQ+ˆQ)=180∘−(35∘+60∘)=85∘.
Vậy ^NPM=^MPQ=35∘, ^QMP=85∘.