Chứng minh rằng: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai
Chứng minh rằng: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.
Chứng minh rằng: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.
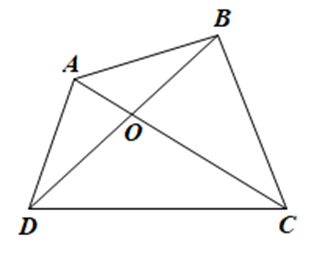
Gọi O là giao điểm của hai đường chéo AC và BD trong tứ giác ABCD.
Xét tam giác OAB, ta có: OA + OB > AB.
Xét tam giác OCD, ta có: OC + OD > CD.
Suy ra OA + OB + OC + OD > AB + CD hay AC + BD > AB + CD.
Tương tự, ta cũng chứng minh được: AC + BD > AD + BC.
Vậy: trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.