Câu hỏi:
19/12/2023 110
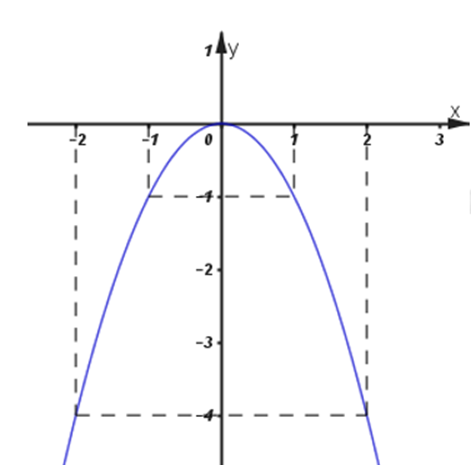
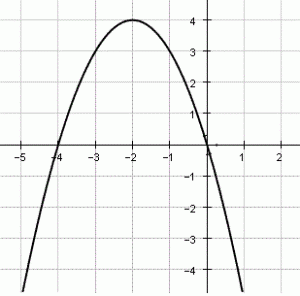
Đồ thị hàm số sau đây là của hàm số bậc hai nào ?

A. y = x2 – 4x + 1;
B. y = x2 – 4x – 2;
C. y = –x2 – 4x;
D. y = x2 – 4x + 3.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: C.
Hàm số bậc hai có dạng y = ax2 + bx + c (a ≠ 0).
Dựa vào hình vẽ, ta thấy đồ thị hàm số y = ax2 + bx + c có bề lõm hướng xuống, đỉnh I(–2; 4) và cắt trục tung tại điểm (0; 0).
Do đó ta có:
a < 0 (1)
\( - \frac{b}{{2a}} = - 2\) (2); \( - \frac{\Delta }{{4a}} = 4 \Leftrightarrow \frac{{{b^2} - 4ac}}{{4a}} = - 4 \Leftrightarrow {b^2} - 4ac = - 16a\) (3)
c = 0 (4)
Thay (4) vào (3) ta có: b2 – 4a.0 = –16a ⇔ b2 + 16a = 0 (5)
Từ (2) ta có: b = 4a (6)
Thay (6) vào (5) ta có: (4a)2 + 16a = 0 ⇔ 16a2 + 16a = 0
⇔ 16a(a + 1) = 0 ⇔ \(\left[ \begin{array}{l}a = 0\,\,(L)\\a = - 1\,\,(TM)\end{array} \right.\)
Với a = –1 ta có: b = 4.(–1) = –4
Vậy hàm số y = ax2 + bx + c là y = –x2 – 4x.
Hướng dẫn giải:
Đáp án đúng là: C.
Hàm số bậc hai có dạng y = ax2 + bx + c (a ≠ 0).
Dựa vào hình vẽ, ta thấy đồ thị hàm số y = ax2 + bx + c có bề lõm hướng xuống, đỉnh I(–2; 4) và cắt trục tung tại điểm (0; 0).
Do đó ta có:
a < 0 (1)
\( - \frac{b}{{2a}} = - 2\) (2); \( - \frac{\Delta }{{4a}} = 4 \Leftrightarrow \frac{{{b^2} - 4ac}}{{4a}} = - 4 \Leftrightarrow {b^2} - 4ac = - 16a\) (3)
c = 0 (4)
Thay (4) vào (3) ta có: b2 – 4a.0 = –16a ⇔ b2 + 16a = 0 (5)
Từ (2) ta có: b = 4a (6)
Thay (6) vào (5) ta có: (4a)2 + 16a = 0 ⇔ 16a2 + 16a = 0
⇔ 16a(a + 1) = 0 ⇔ \(\left[ \begin{array}{l}a = 0\,\,(L)\\a = - 1\,\,(TM)\end{array} \right.\)
Với a = –1 ta có: b = 4.(–1) = –4
Vậy hàm số y = ax2 + bx + c là y = –x2 – 4x.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
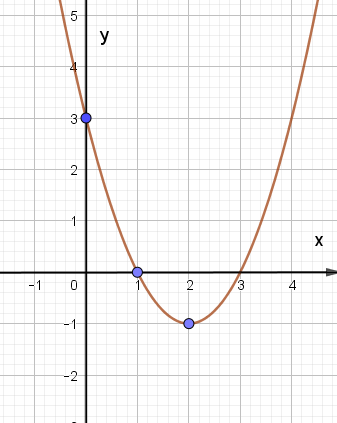
Cho hàm số bậc hai y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới.
Xác định công thức của hàm số đó.
Cho hàm số bậc hai y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới.

Xác định công thức của hàm số đó.
Câu 2:
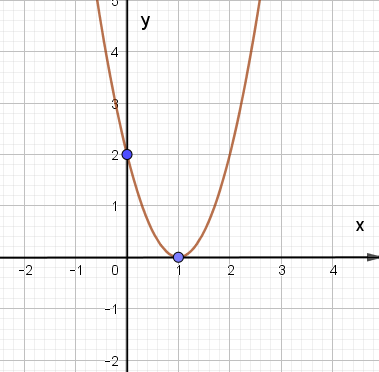
Cho hàm số bậc hai y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới.
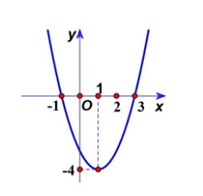
Khi đó 2a + b + 2c bằng:
Cho hàm số bậc hai y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới.

Khi đó 2a + b + 2c bằng:
Câu 3:
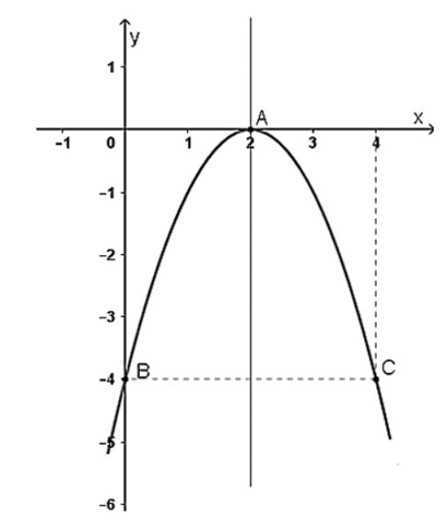
Cho hàm số y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới đây.
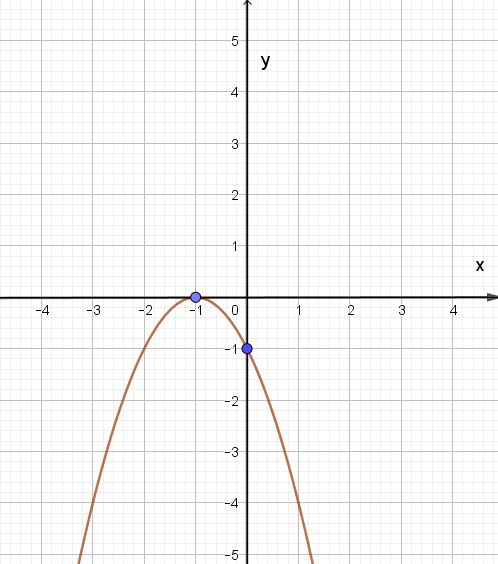
Công thức hàm số của đồ thị trên là:
Cho hàm số y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới đây.

Công thức hàm số của đồ thị trên là:
Câu 4:
Cho hàm số y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới. Xác định hàm số đó.
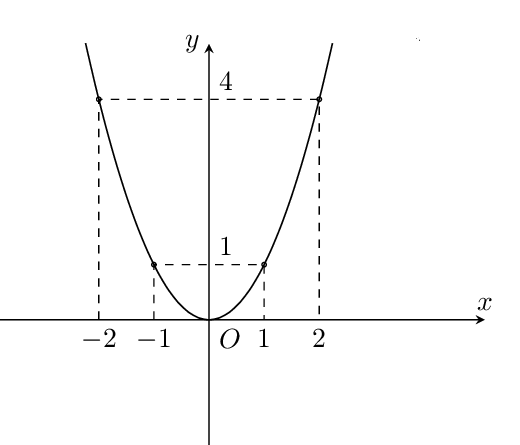
Câu 10:
Cho đồ thị hàm số y = ax2 + bx + c (a ≠ 0) trong hình vẽ sau. Xác định hàm số đó.
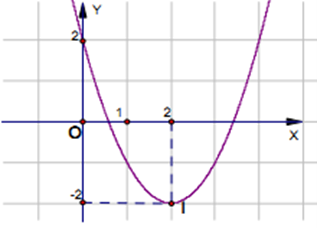
Cho đồ thị hàm số y = ax2 + bx + c (a ≠ 0) trong hình vẽ sau. Xác định hàm số đó.

Câu 11:
Cho hàm số y = ax2 + bx + c (a ≠ 0) có đồ thị là parabol trong hình dưới. Xác định hàm số đó.