Câu hỏi:
29/12/2023 148
Đề thi trắc nghiệm môn Toán gồm 50 câu hỏi, mỗi câu có 4 phương án trả lời trong đó chỉ có một phương án trả lời đúng. Mỗi câu trả lời đúng được 0,2 điểm. Một học sinh không học bài nên mỗi câu trả lời đều chọn ngẫu nhiên một phương án. Xác suất để học sinh đó được đúng 6 điểm là bao nhiêu?
Đề thi trắc nghiệm môn Toán gồm 50 câu hỏi, mỗi câu có 4 phương án trả lời trong đó chỉ có một phương án trả lời đúng. Mỗi câu trả lời đúng được 0,2 điểm. Một học sinh không học bài nên mỗi câu trả lời đều chọn ngẫu nhiên một phương án. Xác suất để học sinh đó được đúng 6 điểm là bao nhiêu?
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Mỗi câu trả lời đúng được 0,2 điểm thì để đạt được 6 điểm cần trả lời đúng 30 câu.
Chọn 30 câu trong 50 câu có: \(C_{50}^{30}\) cách.
Mỗi câu có 4 đáp án nên xác suất đúng là \(\frac{1}{4}\) và xác suất sai là \(\frac{3}{4}\).
Do đó xác suất để học sinh đó được đúng 6 điểm là: \({\left( {\frac{1}{4}} \right)^{30}}.{\left( {\frac{3}{4}} \right)^{20}}.C_{50}^{30}\).
Mỗi câu trả lời đúng được 0,2 điểm thì để đạt được 6 điểm cần trả lời đúng 30 câu.
Chọn 30 câu trong 50 câu có: \(C_{50}^{30}\) cách.
Mỗi câu có 4 đáp án nên xác suất đúng là \(\frac{1}{4}\) và xác suất sai là \(\frac{3}{4}\).
Do đó xác suất để học sinh đó được đúng 6 điểm là: \({\left( {\frac{1}{4}} \right)^{30}}.{\left( {\frac{3}{4}} \right)^{20}}.C_{50}^{30}\).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – 4y – 1 = 0 và điểm I(1; – 2). Gọi (C) là đường tròn tâm I và cắt đường thẳng d tại hai điểm A và B sao cho tam giác IAB có diện tích bằng 4. Viết phương trình đường tròn (C).
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – 4y – 1 = 0 và điểm I(1; – 2). Gọi (C) là đường tròn tâm I và cắt đường thẳng d tại hai điểm A và B sao cho tam giác IAB có diện tích bằng 4. Viết phương trình đường tròn (C).
Câu 2:
Phương tiện bạn Khoa có thể chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt được thể hiện qua sơ đồ cây sau:
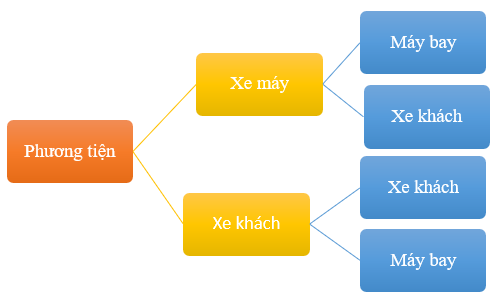
Hỏi bạn Khoa có mấy cách chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt.
Câu 3:
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(– 2; 3) và đi qua điểm A(6; 0). Viết phương trình đường tròn (C).
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(– 2; 3) và đi qua điểm A(6; 0). Viết phương trình đường tròn (C).
Câu 4:
Một đường tròn có tâm I(3; –2), tiếp xúc với đường thẳng ∆: x – 5y + 1 = 0. Bán kính của đường tròn đó bằng:
Một đường tròn có tâm I(3; –2), tiếp xúc với đường thẳng ∆: x – 5y + 1 = 0. Bán kính của đường tròn đó bằng:
Câu 5:
Phương trình tổng quát của đường thẳng đi qua hai điểm A(–2; 4) và B(1; 0) là:
Câu 6:
Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:
Năng suất lúa (tạ/ha)
25
30
35
40
45
Tần số
4
7
9
6
5
So sánh Q1 và Q2 ?
Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:
|
Năng suất lúa (tạ/ha) |
25 |
30 |
35 |
40 |
45 |
|
Tần số |
4 |
7 |
9 |
6 |
5 |
So sánh Q1 và Q2 ?
Câu 7:
Thời gian chạy 50 m của 20 học sinh được ghi lại trong bảng dưới đây:

Khoảng biến thiên của bảng số liệu trên là:
Thời gian chạy 50 m của 20 học sinh được ghi lại trong bảng dưới đây:

Khoảng biến thiên của bảng số liệu trên là:
Câu 8:
Cho tập A có n phần tử (n ∈ ℕ, n ≥ 2), k là số nguyên thỏa mãn 1 ≤ k ≤ n. Số các chỉnh hợp chập k của n phần tử trên là:
Cho tập A có n phần tử (n ∈ ℕ, n ≥ 2), k là số nguyên thỏa mãn 1 ≤ k ≤ n. Số các chỉnh hợp chập k của n phần tử trên là:
Câu 9:
41 học sinh của một lớp kiểm tra chất lượng đầu năm thang điểm 30. Kết quả như sau:
Điểm
9
11
14
16
17
18
20
21
23
25
Số lượng (tần số)
3
6
4
4
6
7
3
4
2
2
Phương sai của bảng số liệu trên là:
41 học sinh của một lớp kiểm tra chất lượng đầu năm thang điểm 30. Kết quả như sau:
|
Điểm |
9 |
11 |
14 |
16 |
17 |
18 |
20 |
21 |
23 |
25 |
|
Số lượng (tần số) |
3 |
6 |
4 |
4 |
6 |
7 |
3 |
4 |
2 |
2 |
Phương sai của bảng số liệu trên là:
Câu 10:
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(–1; –2) và N(–3; 2). Tọa độ trung điểm I của đoạn thẳng MN là:
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(–1; –2) và N(–3; 2). Tọa độ trung điểm I của đoạn thẳng MN là:
Câu 11:
Cho nhị thức \({\left( {2{x^2} + \frac{1}{{{x^3}}}} \right)^n}\), trong đó số nguyên \(n\) thỏa mãn \(A_n^3 = 12n\). Tìm số hạng chứa x5 trong khai triển.
Cho nhị thức \({\left( {2{x^2} + \frac{1}{{{x^3}}}} \right)^n}\), trong đó số nguyên \(n\) thỏa mãn \(A_n^3 = 12n\). Tìm số hạng chứa x5 trong khai triển.
Câu 12:
Phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình đường tròn khi và chỉ khi:
Phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình đường tròn khi và chỉ khi:
Câu 13:
Cho 8 điểm phân biệt nằm trong mặt phẳng. Hỏi có bao nhiêu đoạn thẳng có hai đầu mút là hai trong 8 điểm đó.
Cho 8 điểm phân biệt nằm trong mặt phẳng. Hỏi có bao nhiêu đoạn thẳng có hai đầu mút là hai trong 8 điểm đó.
Câu 15:
Gieo một đồng xu ba lần liên tiếp. Xác suất để xuất hiện ít nhất một lần mặt ngửa là:
Gieo một đồng xu ba lần liên tiếp. Xác suất để xuất hiện ít nhất một lần mặt ngửa là:


