Câu hỏi:
03/04/2024 67
Có hai dãy ghế ngồi đối diện nhau, mỗi dãy gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh lớp 11A và 6 học sinh lớp 11B vào hai dãy ghế trên. Có bao nhiêu cách xếp để hai học sinh ngồi đối diện là khác lớp.
Có hai dãy ghế ngồi đối diện nhau, mỗi dãy gồm 6 ghế. Xếp ngẫu nhiên 6 học sinh lớp 11A và 6 học sinh lớp 11B vào hai dãy ghế trên. Có bao nhiêu cách xếp để hai học sinh ngồi đối diện là khác lớp.
A. 33177600.
B. 239500800.
C.518400.
D.1036800.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
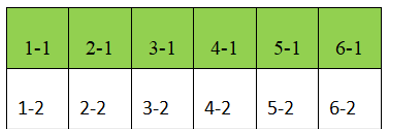
Đánh số ghế như hình vẽ. Khi đó, chúng ta tiến hành xếp chỗ cho 12 học sinh đó như sau:
+ Ghế 1-1 có thể xếp bất kì học sinh của lớp nào cũng được. Do đó có: 6 + 6 = 12( cách xếp).
+ Ghế 1-2 có thể xếp học sinh của lớp chưa ngồi ở ghế 1-1. Do đó có 6 (cách xếp).
+ Ghế 2-1 có thể xếp bất kì học sinh của lớp nào cũng được trừ 2 học sinh đã được xếp chỗ. Do đó có: 12 - 2 = 10( cách xếp).
+ Ghế 2-2 có thể xếp học sinh của lớp chưa ngồi ở ghế 2-1. Do đó có 5 (cách xếp).
+ Ghế 3-1 có thể xếp bất kì học sinh của lớp nào cũng được trừ 4 học sinh đã được xếp chỗ. Do đó có: 12- 4 = 8( cách xếp).
+ Ghế 3-2 có thể xếp học sinh của lớp chưa ngồi ở ghế 3-1. Do đó có 4 (cách xếp).
+ Ghế 4-1 có thể xếp bất kì học sinh của lớp nào cũng được trừ 6 học sinh đã được xếp chỗ. Do đó có: 12 - 6 = 6( cách xếp).
+ Ghế 4-2 có thể xếp học sinh của lớp chưa ngồi ở ghế 4-1. Do đó có 3 (cách xếp).
+ Ghế 5-1 có thể xếp bất kì học sinh của lớp nào cũng được trừ 8 học sinh đã được xếp chỗ. Do đó có: 12- 8 = 4( cách xếp).
+ Ghế 5-2 có thể xếp học sinh của lớp chưa ngồi ở ghế 5-1. Do đó có 2 (cách xếp).
+ Ghế 6-1 có thể xếp bất kì học sinh của lớp nào cũng được trừ 10 học sinh đã được xếp chỗ. Do đó có: 12 - 10 = 2( cách xếp).
+ Ghế 6-2 chỉ có thể xếp học sinh của lớp chưa ngồi ở ghế 6-1. Do đó chỉ còn có  (cách xếp).
(cách xếp).
Vậy, theo qui tắc nhân số cách xếp để hai học sinh ngồi đối diện là khác lớp là:
12.6.10.5.8.4.6.3.4.2.2.1=33177600 (cách xếp)
Cách 2:
Xếp 6 học sinh lớp 11A vào dãy ghế thứ nhất thì có 6! cách xếp.
Xếp 6 học sinh lớp 11B vào dãy ghế thứ hai thì có 6! cách xếp.
Ở các cặp ghế đối diện nhau hai bạn học sinh lớp 11A và học sinh lớp 11B có thể đổi chỗ cho nhau nên có 26 cách xếp.
Vậy, số cách xếp để hai học sinh ngồi đối diện là khác lớp là:6!.6!.26=33177600(cách xếp).
Chọn A
Đánh số ghế như hình vẽ. Khi đó, chúng ta tiến hành xếp chỗ cho 12 học sinh đó như sau:
+ Ghế 1-1 có thể xếp bất kì học sinh của lớp nào cũng được. Do đó có: 6 + 6 = 12( cách xếp).
+ Ghế 1-2 có thể xếp học sinh của lớp chưa ngồi ở ghế 1-1. Do đó có 6 (cách xếp).
+ Ghế 2-1 có thể xếp bất kì học sinh của lớp nào cũng được trừ 2 học sinh đã được xếp chỗ. Do đó có: 12 - 2 = 10( cách xếp).
+ Ghế 2-2 có thể xếp học sinh của lớp chưa ngồi ở ghế 2-1. Do đó có 5 (cách xếp).
+ Ghế 3-1 có thể xếp bất kì học sinh của lớp nào cũng được trừ 4 học sinh đã được xếp chỗ. Do đó có: 12- 4 = 8( cách xếp).
+ Ghế 3-2 có thể xếp học sinh của lớp chưa ngồi ở ghế 3-1. Do đó có 4 (cách xếp).
+ Ghế 4-1 có thể xếp bất kì học sinh của lớp nào cũng được trừ 6 học sinh đã được xếp chỗ. Do đó có: 12 - 6 = 6( cách xếp).
+ Ghế 4-2 có thể xếp học sinh của lớp chưa ngồi ở ghế 4-1. Do đó có 3 (cách xếp).
+ Ghế 5-1 có thể xếp bất kì học sinh của lớp nào cũng được trừ 8 học sinh đã được xếp chỗ. Do đó có: 12- 8 = 4( cách xếp).
+ Ghế 5-2 có thể xếp học sinh của lớp chưa ngồi ở ghế 5-1. Do đó có 2 (cách xếp).
+ Ghế 6-1 có thể xếp bất kì học sinh của lớp nào cũng được trừ 10 học sinh đã được xếp chỗ. Do đó có: 12 - 10 = 2( cách xếp).
+ Ghế 6-2 chỉ có thể xếp học sinh của lớp chưa ngồi ở ghế 6-1. Do đó chỉ còn có ![]() (cách xếp).
(cách xếp).
Vậy, theo qui tắc nhân số cách xếp để hai học sinh ngồi đối diện là khác lớp là:
12.6.10.5.8.4.6.3.4.2.2.1=33177600 (cách xếp)
Cách 2:
Xếp 6 học sinh lớp 11A vào dãy ghế thứ nhất thì có 6! cách xếp.
Xếp 6 học sinh lớp 11B vào dãy ghế thứ hai thì có 6! cách xếp.
Ở các cặp ghế đối diện nhau hai bạn học sinh lớp 11A và học sinh lớp 11B có thể đổi chỗ cho nhau nên có 26 cách xếp.
Vậy, số cách xếp để hai học sinh ngồi đối diện là khác lớp là:6!.6!.26=33177600(cách xếp).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Từ các số 1,2,3,4,5,6,7,8,9 lập được bao nhiêu số có ba chữ số khác nhau bé hơn 345?
Câu 2:
Có bao nhiêu cách chia 80 đồ vật giống nhau cho 5 người sao cho mỗi người được ít nhất 5 đồ vật?
Có bao nhiêu cách chia 80 đồ vật giống nhau cho 5 người sao cho mỗi người được ít nhất 5 đồ vật?
Câu 4:
Điều kiện của tham số m để phương trình sin(2019x−150)−m=0 vô nghiệm là:
Điều kiện của tham số m để phương trình sin(2019x−150)−m=0 vô nghiệm là:
Câu 6:
Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng (d):2x+3y+5=0 . Qua phép đối xứng trục Ox, phương trình ảnh của đường thẳng (d) là
Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng (d):2x+3y+5=0 . Qua phép đối xứng trục Ox, phương trình ảnh của đường thẳng (d) là
Câu 8:
Tìm điều kiện của tham số m để phương trình sin4x−4cos2x−msin2x+2m=0có hai nghiệm phân biệt thuộc đoạn [−3π8;π6].
Câu 9:
Trong mặt phẳng với hệ tọa độ Oxy, một phép vi tự hệ số k = 2 biến A(1;3) thuộc đường tròn (C) thành A'(-4;6) thuộc đường tròn (C'). Phương trình tiếp tuyến của (C) tại A là y = x + 2. Hỏi phương trình tiếp tuyến của (C') tại A' là:
Trong mặt phẳng với hệ tọa độ Oxy, một phép vi tự hệ số k = 2 biến A(1;3) thuộc đường tròn (C) thành A'(-4;6) thuộc đường tròn (C'). Phương trình tiếp tuyến của (C) tại A là y = x + 2. Hỏi phương trình tiếp tuyến của (C') tại A' là:
Câu 10:
Tính tổng tất cả các số có 5 chữ số khác nhau được lập từ tập A={0; 2; 3; 5; 6; 7}.
Tính tổng tất cả các số có 5 chữ số khác nhau được lập từ tập A={0; 2; 3; 5; 6; 7}.
Câu 11:
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 4cos 2x + 1 lần lượt là:
Câu 12:
Cho tập A={1;2;3;4;6;7;9} có bao nhiêu số tự nhiên chẵn gồm 4 chữ số khác nhau được lấy từ các chữ số của tập A .
Cho tập A={1;2;3;4;6;7;9} có bao nhiêu số tự nhiên chẵn gồm 4 chữ số khác nhau được lấy từ các chữ số của tập A .
Câu 13:
Trong khoảng (0 ; π2) phương trình sin24x+3sin4xcos4x−4cos24x=0 có số nghiệm là:
Trong khoảng (0 ; π2) phương trình sin24x+3sin4xcos4x−4cos24x=0 có số nghiệm là:


