Chứng minh rằng các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền

Bài 88 trang 94 SBT Toán 7 Tập 2: Chứng minh rằng các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.

Trả lời

Lời giải

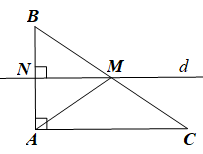
Gọi d là đường trung trực của cạnh AB và M là giao điểm của d và BC.

Do M ∈ d nên MA = MB hay tam giác MAB cân tại M.

Suy ra $\widehat{MBA}=\widehat{MAB}$ (1)

Trong tam giác vuông ABC có $\widehat{ABC}+\widehat{ACB}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Nên $\widehat{ACB}=90°-\widehat{ABC}$ (2)

Ta có $\widehat{BAM}+\widehat{MAC}=\widehat{BAC}=90°$

Nên $\widehat{MAC}=90°-\widehat{MBA}$ (3)

Từ (1), (2) và (3) suy ra $\widehat{MAC}=\widehat{MCA}$

Do đó tam giác MAC cân tại M nên MA = MC.

Như vậy, MB = MC (= MA) nên M là trung điểm của BC.

Vậy các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 9. Đường trung trực của một đoạn thẳng

Bài 10. Tính chất ba đường trung tuyến của tam giác

Bài 11. Tính chất ba đường phân giác của tam giác

Bài 12. Tính chất ba đường trung trực của tam giác

Bài 13. Tính chất ba đường cao của tam giác

Bài tập cuối chương 7