Cho tam giác ABC cân ở A có góc BAC = 120 độ  . Đường trung trực của các cạnh AB và AC cắt nhau ở I và cắt cạnh BC lần lượt tại D, E (Hình 56).

Bài 90 trang 95 SBT Toán 7 Tập 2: Cho tam giác ABC cân ở A có $\widehat{BAC}=120°$. Đường trung trực của các cạnh AB và AC cắt nhau ở I và cắt cạnh BC lần lượt tại D, E (Hình 56).

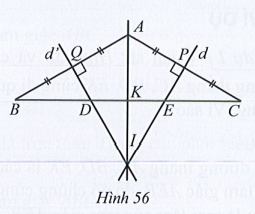
a) Chứng minh điểm I nằm trên đường trung trực của đoạn thẳng DE.

b) Đường tròn tâm I bán kính IA đi qua những điểm nào?

c) Tính số đo các góc của tam giác IBC.

Trả lời

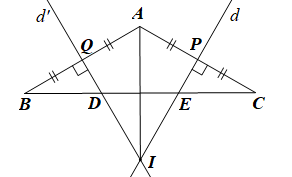
a) Gọi P và Q lần lượt là giao điểm của hai đường trung trực d, d’ với AC, AB.

• Vì tam giác ABC cân tại A nên AB = AC, $\widehat{B}=\widehat{C}$.

Vì Q là trung điểm của AB nên AQ = QB = $\frac{1}{2}$AB.

Vì P là trung điểm của AC nên AP = PC = $\frac{1}{2}$AC.

Mà AB = AC nên AQ = BQ = AP = CP.

• Xét ∆AQI và ∆API có:

$\widehat{AQI}=\widehat{API}\left(=90°\right)$,

AI là cạnh chung,

AQ = AP (chứng minh trên)

Do đó ∆AQI = ∆API (cạnh huyền – cạnh góc vuông).

Do đó QI = PI (hai cạnh tương ứng).

• Xét ∆BQD và ∆CPE có:

$\widehat{BQ\text{D}}=\widehat{CPE}\left(=90°\right)$,

$\widehat{B}=\widehat{C}$ (chứng minh trên),

BQ = CP (chứng minh trên)

Do đó ∆BQD = ∆CPE (cạnh góc vuông – góc nhọn kề).

Suy ra QD = PE (hai cạnh tương ứng).

• Ta có: QI = QD + DI và PI = PE + EI.

Mà QI = PI và QD = PE (chứng minh trên)

Do đó DI = EI nên điểm I nằm trên đường trung trực của đoạn thẳng DE.

Vậy điểm I nằm trên đường trung trực của đoạn thẳng DE.

b) Vì I nằm trên đường trung trực của AB nên IA = IB.

Vì I nằm trên đường trung trực của AC nên IA = IC.

Suy ra IA = IB = IC

Nên đường tròn tâm I bán kính IA đi qua các điểm A, B, C

Vậy đường tròn tâm I bán kính IA đi qua các điểm A, B, C.

c) Vì ∆AQI = ∆API (chứng minh câu a)

Nên $\widehat{QAI}=\widehat{PAI}$ (hai góc tương ứng)

Do đó AI là tia phân giác của góc BAC và $\widehat{BAI}=\widehat{CAI}=\frac{1}{2}\widehat{BAC}=\frac{1}{2}.120°=60°$

Xét tam giác ABI có IA = IB (chứng minh câu b) nên tam giác ABI cân tại I.

Lại có $\widehat{BAI}=60°$ nên tam giác ABI là tam giác đều.

Do đó IA = IB = AB.

Mà AB = AC, IA = IB = IC nên IA = IB = IC = AB = AC.

Xét $∆$BAC và $∆$BIC có:

AB = IB (chứng minh trên),

AC = IC (chứng minh trên),

BC là cạnh chung

Do đó ∆BAC = ∆BIC (c.c.c)

Suy ra $\widehat{ABC}=\widehat{IBC},\widehat{BAC}=\widehat{BIC}\widehat{,ACB}=\widehat{ICB}$ (các cặp góc tương ứng)

Xét ∆ABC có $\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180°$ (tổng ba góc của một tam giác).

Mà $\widehat{BAC}=120°$ (giả thiết) và $\widehat{ABC}=\widehat{ACB}$ (do ∆ABC cân tại A).

Suy ra $\widehat{ABC}=\widehat{ACB}=\frac{180°-\widehat{BAC}}{2}=\frac{180°-120°}{2}=30°$.

Do đó $\widehat{IBC}=\widehat{ICB}=30°,\widehat{BIC}=120°$

Vậy $\widehat{IBC}=\widehat{ICB}=30°,\widehat{BIC}=120°$.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 9. Đường trung trực của một đoạn thẳng

Bài 10. Tính chất ba đường trung tuyến của tam giác

Bài 11. Tính chất ba đường phân giác của tam giác

Bài 12. Tính chất ba đường trung trực của tam giác

Bài 13. Tính chất ba đường cao của tam giác

Bài tập cuối chương 7