Cho tứ giác ABCD có P là giao điểm của hai đường chéo. Giải thích tại sao AB // CD và AD // BC trong mỗi trường hợp sau:

Trường hợp 1: AB = CD và AD = BC (Hình 7a).

Trường hợp 2: AB // CD và AB = CD (Hình 7b).

Trường hợp 3: AD // BC và AD = BC (Hình 7c).

Trường hợp 4: $\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}$ (Hình 7d).

Trường hợp 5: PA = PC, PB = PD (Hình 7e).

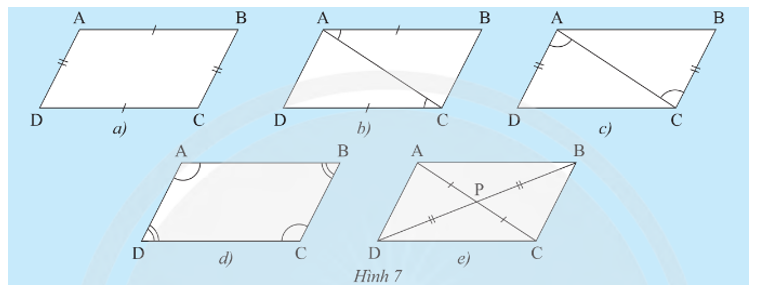
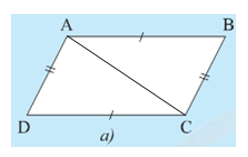
• Hình 7a):

Xét DABC và DCDA có:

AB = CD; BC = DA; AC là cạnh chung

Do đó DABC = DCDA (c.c.c)

Suy ra $\widehat{BAC}=\widehat{DCA}$ và $\widehat{BCA}=\widehat{DAC}$ (các cặp góc tương ứng).

Vì $\widehat{BAC}=\widehat{DCA}$ và hai góc này ở vị trí so le trong nên AB // CD.

Vì $\widehat{BCA}=\widehat{DAC}$ và hai góc này ở vị trí so le trong nên AD // BC.

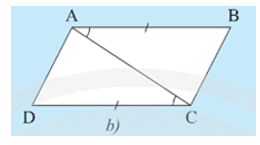
• Hình 7b):

Ta có $\widehat{BAC}=\widehat{DCA}$ và hai góc này ở vị trí so le trong nên AB // CD.

Xét DABC và DCDA có:

AC là cạnh chung; $\widehat{BAC}=\widehat{DCA}$; AB = CD

Do đó DABC = DCDA (c.g.c)

Suy ra $\widehat{BCA}=\widehat{DAC}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên AD // BC.

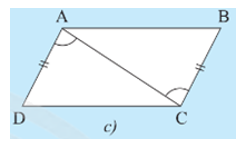
• Hình 7c):

Ta có: $\widehat{BCA}=\widehat{DAC}$ và hai góc này ở vị trí so le trong nên AD // BC.

Xét DABC và DCDA có:

AC là cạnh chung; $\widehat{BCA}=\widehat{DAC}$; BC = AD

Do đó DABC = DCDA (c.g.c)

Suy ra $\widehat{BAC}=\widehat{DCA}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên AB // CD.

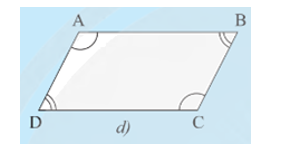
• Hình 7d):

Xét tứ giác ABCD ta có $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360°$ (định lí tổng các góc của một tứ giác)

Mà $\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}$ nên ta có $\widehat{A}+\widehat{B}+\widehat{A}+\widehat{B}=360°$

Suy ra $\widehat{A}+\widehat{B}=\frac{360°}{2}=180°$ và $\widehat{A}+\widehat{D}=180°$

Do đó AD // BC và AB // CD.

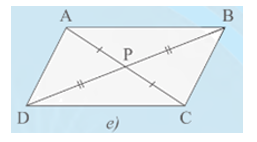
• Hình 7e):

Xét DPAB và DPCD có:

PA = PC; $\widehat{APB}=\widehat{CPD}$ (đối đỉnh); PB = PD

Do đó DPAB = DPCD (c.g.c)

Suy ra $\widehat{BAP}=\widehat{DCP}$ (hai góc tương ứng)

Hay $\widehat{BAC}=\widehat{DCA}$, mà hai góc này ở vị trí so le trong nên AB // CD.

Tương tự ta cũng chứng minh được DPAD = DPCB (c.g.c)

Suy ra $\widehat{DAP}=\widehat{BCP}$ (hai góc tương ứng)

Hay $\widehat{DAC}=\widehat{BCA}$, mà hai góc này ở vị trí so le trong nên AD // BC.