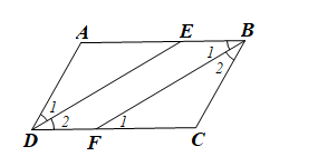
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F.

a) Chứng minh DE // BF.

a)

Do ABCD là hình bình hành nên AB // CD và $\widehat{B}=\widehat{D}$.

Vì DE là tia phân giác của góc D nên ${\widehat{D}}_1={\widehat{D}}_2=\frac{1}{2}\widehat{D}$.

Vì BF là tia phân giác của góc B nên ${\widehat{B}}_1={\widehat{B}}_2=\frac{1}{2}\widehat{B}$.

Do đó ${\widehat{B}}_1={\widehat{D}}_2$.

Do AB // CD nên ${\widehat{B}}_1={\widehat{F}}_1$ (so le trong).

Suy ra ${\widehat{D}}_2={\widehat{F}}_1$

Mà hai góc này ở vị trí so le trong nên DE // BF.