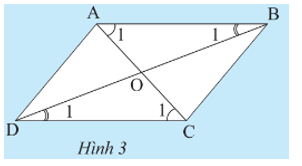
Cho tứ giác ABCD có các cạnh đối song song. Gọi O là giao điểm của hai đường chéo. Hãy chứng tỏ:

‒ Tam giác ABC bằng tam giác CDA.

‒ Tam giác OAB bằng tam giác OCD.

• Tứ giác ABCD có AB // DC và AD // BC.

Từ AB // DC suy ra ${\widehat{A}}_1={\widehat{C}}_1$ (so le trong) và ${\widehat{B}}_1={\widehat{D}}_1$ (so le trong).

Từ AD // BC suy ra ${\widehat{A}}_2={\widehat{C}}_2$ (so le trong).

Xét DABC và DCDA có:

${\widehat{A}}_1={\widehat{C}}_1$; AC là cạnh chung; ${\widehat{A}}_2={\widehat{C}}_2$

Do đó DABC = DCDA (g.c.g).

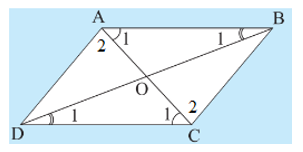
• Do DABC = DCDA nên AB = CD (hai cạnh tương ứng).

Xét DOAB và DOCD có:

${\widehat{A}}_1={\widehat{C}}_1$; AB = CD; ${\widehat{B}}_1={\widehat{D}}_1$ (chứng minh trên)

Do đó DOAB = DOCD (g.c.g).